Topological equivalence of the 2-sphere and the extended complex plane (the `Riemann sphere’)

In this short note I want to quickly set out the mathematical details of how the Riemann sphere arises when the point at infinity is added to the complex plane to give the extended complex plane $\Sigma = \mathbb{C}\bigcup \{\infty \}$ , i.e., an explicit homeomorphism which establishes the topological equivalence of the $2$ -sphere and the extended complex plane, giving rise to the name Riemann sphere for the latter.

The $2$ -sphere in $\mathbb{R}^3$ , namely

$S^2 = \{(x_1, x_2, x_3) \in \mathbb{R}^3| x_1^2 + x_2^2 + x_3^2 = 1 \}$

is visualised as sitting in a coordinate system with its centre at the origin, and the complex plane $\mathbb{C}$ is identified with the plane $x_3 = 0$ by identifying $z = x + iy$ , $x, y \in \mathbb{R}$ , with $(x, y, 0)$ for all $z \in \mathbb{C}$ . The point $N = (0, 0, 1)$ is identified as the `north pole’ of $S^2$ , and stereographic projections from $N$ then give rise to a bijective map between $S^2 \backslash \{N \}$ and $\mathbb{C}$ of the form

$\pi: S^2\backslash \{N \} \rightarrow \mathbb{C}$

$\pi: Q \mapsto P$

such that the points $N$ , $Q$ , and $P$ are collinear (but note that we are excluding $N$ from the domain of the bijection at this stage). The situation is illustrated in the following diagram:

To show that $\pi$ is in fact a homeomorphism (i.e., a continuous bijection from $S^2\backslash \{N \}$ to $\mathbb{C}$ whose inverse is also continuous), let $P = (x, y, 0)$ where $z = x + iy \in \mathbb{C}$ , and let

$Q = (x_1, x_2, x_3) \in S^2 \backslash \{N \}$

Since $P$ , $Q$ , and $N$ are collinear, there is some constant $t$ such that

$P = N + t(Q - N)$

Therefore considering the coordinates separately in this equation we have

$\frac{x}{x_1} = t$

$\frac{y}{x_2} = t$

$\frac{1}{1 - x_3} = t$

and so

$x = \frac{x_1}{1-x_3}$

$y = \frac{x_2}{1-x_3}$

Therefore we have

$z = x + iy = \frac{x_1 + ix_2}{1 - x_3}$

and this is the map $\pi: Q \mapsto P$ .

To get the inverse map $\pi^{-1}: P \mapsto Q$ , we observe that

$x^2 + y^2 + 1$

$= \frac{x_1^2}{(1-x_3)^2} + \frac{x_2^2}{(1-x_3)^2} + \frac{(1-x_3)^2}{(1-x_3)^2}$

$= \frac{1 - x_3^2}{(1-x_3)^2} + \frac{1 - 2x_3 + x_3^2}{(1-x_3)^2}$

(using $x_1^2 + x_2^2 + x_3^2 = 1$ )

$= \frac{2 - 2x_3}{(1-x_3)^2}$

$= \frac{2}{1-x_3}$

Therefore $\pi^{-1}: P \mapsto Q$ is given by

$x_1 = x(1-x_3) = \frac{2x}{x^2 + y^2 + 1}$

$x_2 = y(1-x_3) = \frac{2y}{x^2 + y^2 + 1}$

$1 - x_3 = \frac{2}{x^2 + y^2 + 1}$ $\qquad$ $\implies$ $\qquad$ $x_3 = \frac{x^2 + y^2 - 1}{x^2 + y^2 + 1}$

These expressions show that both $\pi$ and $\pi^{-1}$ are continuous, so $\pi$ is a homeomorphism between $S^2\backslash \{N \}$ and $\mathbb{C}$ , i.e., $S^2\backslash \{N \}$ and $\mathbb{C}$ are topologically equivalent.

To complete the picture we need to extend the homeomorphism $\pi$ to include the point $N$ . We do this by defining

$\pi(N) = \infty$

where $\infty$ , known as the point at infinity, is the distinguishing feature that makes the geometry of the present context non-Euclidean (it can be viewed as the point in this geometry where lines which start out parallel eventually meet, something which is impossible in Euclidean geometry). With the addition of the point at infinity into the picture we get the full homeomorphism

$\pi: S^2 \rightarrow \Sigma$

between the $2$ -sphere and the extended complex plane. This explains why the extended complex plane $\Sigma$ is referred to as the Riemann sphere. It is because the extended complex plane is homeomorphic (i.e., topologically equivalent) to the $2$ -sphere in $\mathbb{R}^3$ .

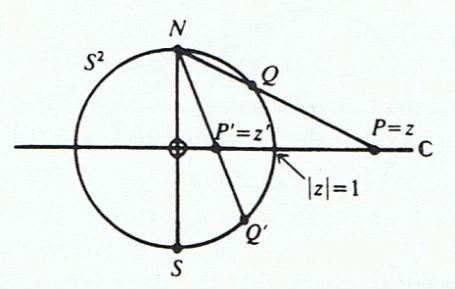
Intuitively, points $Q$ on the $2$ -sphere $S^2$ which are close to the north pole $N$ correspond under $\pi$ to complex numbers $P = z$ with large magnitude $|z|$ , i.e., to complex numbers which are `closer to infinity’ in a sense. Similarly, points $Q^{\prime}$ on the $2$ -sphere which are close to the south pole $S = (0, 0, -1)$ correspond to complex numbers $z^{\prime}$ with small magnitude $|z^{\prime}|$ . Points on the equator of the $2$ -sphere, which intersects the plane $x_3 = 0$ , correspond to the unit circle $|z| = 1$ in the complex plane. The situation is illustrated in the following diagram: