Changing variables in the square of the angular momentum operator

A particle of mass $m$ with position vector $\mathbf{r}$ and velocity $\mathbf{v}$ (with respect to some specified origin) has a linear momentum vector $\mathbf{p} = m \mathbf{v}$ and angular momentum vector

$\mathbf{L} = \mathbf{r} \times \mathbf{p} = m \mathbf{r} \times \mathbf{v}$

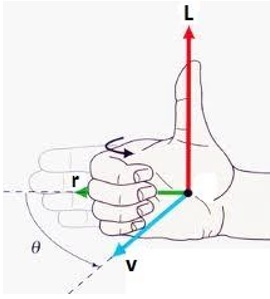
where $\times$ is the vector product operation. The magnitude of the angular momentum vector is $L = rmv\sin \theta$ where $\theta$ is the angle between $\mathbf{r}$ and $\mathbf{v}$ . The direction of $\mathbf{L}$ is given by the right-hand rule when the vectors $\mathbf{r}$ and $\mathbf{v}$ are placed with their tails at the same point: one curls the fingers of the right hand in the direction of rotation of $\mathbf{r}$ into $\mathbf{v}$ and the thumb then points in the direction of $\mathbf{L}$ .

One can find the components of $\mathbf{L}$ in the $x$ , $y$ and $z$ directions in Cartesian coordinates using

$\mathbf{L} = \mathbf{r} \times \mathbf{p}$

$= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \ \\x & y & z \\ \ \\p_x & p_y & p_z \end{vmatrix}$

$= (yp_z - zp_y)\mathbf{i} + (zp_x - xp_z)\mathbf{j} + (xp_y - yp_x)\mathbf{k}$

Therefore the components of $\mathbf{L}$ in Cartesian coordinates are

$L_x = yp_z - zp_y$

$L_y = zp_x - xp_z$

$L_z = xp_y - yp_x$

In classical mechanics the angular momentum magnitude $L$ can take a continuum of values but in quantum mechanics only certain discrete values for $L$ are permissible. Furthermore, the linear momentum vector $\mathbf{p}$ appearing in $\mathbf{L}$ must obey Heisenberg’s uncertainty principle in each direction, i.e.,

$\Delta x \Delta p_x \geq \frac{\hbar}{2}$

in the $x$ -direction and similarly for the $y$ and $z$ directions. These features of quantized variables like $\mathbf{p}$ and $\mathbf{L}$ make it necessary to do calculations with them in quantum mechanics using their operator representations. (For example, on the quantum scale one cannot calculate the expectation of momentum in the $x-$ direction using an integral involving momentum as a function of $x$ because no such function can exist: Heisenberg’s uncertainty principle prevents accurate knowledge of momentum when the value of $x$ is known exactly. One must therefore use the operator representation of momentum rather than momentum as some function of $x$ in order to calculate the expectation). It is a basic postulate of quantum mechanics that every observable quantity characterising a physical system can be represented by a quantum mechanical operator obtained by expressing the quantity in terms of $\mathbf{r}$ and $\mathbf{p}$ and then replacing the vector $\mathbf{p}$ by $- i \hbar \nabla$ where

$\nabla = \mathbf{i} \frac{\partial}{\partial x} + \mathbf{j} \frac{\partial}{\partial y} + \mathbf{k} \frac{\partial}{\partial z}$

and its components $p_x$ , $p_y$ and $p_z$ by

$p_x = - i \hbar \frac{\partial}{\partial x}$

$p_y = - i \hbar \frac{\partial}{\partial y}$

$p_z = - i \hbar \frac{\partial}{\partial z}$

Taking this on board we can then write $\mathbf{L}$ and $L_x$ , $L_y$ and $L_z$ in quantum mechanical operator form in Cartesian coordinates as

$\mathbf{L} = - i \hbar (\mathbf{r} \times \nabla)$

$L_x = - i \hbar \big( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \big)$

$L_y = - i \hbar \big( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z} \big)$

$L_x = - i \hbar \big( x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \big)$

In order to perform some calculations involving Schrödinger’s equation I needed to employ the square of the quantum mechanical angular momentum operator $L^2$ , but in spherical polar coordinates rather than Cartesian coordinates, where

$L^2 = L_x^2 + L_y^2 + L_z^2$

I used the matrix calculus approach in my previous note to achieve the necessary change of variables in $L^2$ . In the present note I want to record the details of this calculation as I have never seen this approach used elsewhere. (This change of variables can also be done using a scale factor method based on vector calculus which I will not go into here).

As in my previous note we begin the matrix calculus approach with the standard conversion equations for spherical polar coordinates:

$x = r \sin \theta \cos \phi$

$y = r \sin \theta \sin \phi$

$z = r \cos \theta$

Differentiating with respect to the vector $(r, \theta, \phi)$ we get

$\begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} & \frac{\partial z}{\partial r}\\ \\ \ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta}\\ \\ \ \frac{\partial x}{\partial \phi} & \frac{\partial y}{\partial \phi} & \frac{\partial z}{\partial \phi}\end{bmatrix} = \begin{bmatrix} \sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta\\ \\ \ r \cos \theta \cos \phi & r \cos \theta \sin \phi & - r \sin \theta\\ \\ \ - r \sin \theta \sin \phi & r \sin \theta \cos \phi & 0\end{bmatrix}$

We can then use the matrix version of the chain rule to write

$\begin{bmatrix} \frac{\partial F}{\partial r}\\ \\ \ \frac{\partial F}{\partial \theta} \\ \\ \ \frac{\partial F}{\partial \phi}\end{bmatrix} = \begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} & \frac{\partial z}{\partial r}\\ \\ \ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta}\\ \\ \ \frac{\partial x}{\partial \phi} & \frac{\partial y}{\partial \phi} & \frac{\partial z}{\partial \phi}\end{bmatrix} \begin{bmatrix} \frac{\partial F}{\partial x}\\ \\ \ \frac{\partial F}{\partial y} \\ \\ \ \frac{\partial F}{\partial z} \end{bmatrix} = \begin{bmatrix} \sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta\\ \\ \ r \cos \theta \cos \phi & r \cos \theta \sin \phi & - r \sin \theta\\ \\ \ - r \sin \theta \sin \phi & r \sin \theta \cos \phi & 0\end{bmatrix} \begin{bmatrix} \frac{\partial F}{\partial x}\\ \\ \ \frac{\partial F}{\partial y} \\ \\ \ \frac{\partial F}{\partial z} \end{bmatrix}$

We can solve this system by inverting the coefficient matrix to get

$\begin{bmatrix} \frac{\partial F}{\partial x}\\ \\ \ \frac{\partial F}{\partial y} \\ \\ \ \frac{\partial F}{\partial z}\end{bmatrix} = \begin{bmatrix} \sin \theta \cos \phi & \frac{\cos \theta \cos \phi}{r} & -\frac{\sin \phi}{r \sin \theta}\\ \\ \ \sin \theta \sin \phi & \frac{\cos \theta \sin \theta}{r} & \frac{\cos \phi}{r \sin \theta}\\ \\ \ \cos \theta & -\frac{\sin \theta}{r} & 0\end{bmatrix} \begin{bmatrix} \frac{\partial F}{\partial r}\\ \\ \ \frac{\partial F}{\partial \theta} \\ \\ \ \frac{\partial F}{\partial \phi} \end{bmatrix}$

Using the equations in this system together with the standard conversion equations we then have

$y \frac{\partial F}{\partial z} = r \sin \theta \sin \phi \big( \cos \theta \frac{\partial F}{\partial r} - \frac{\sin \theta}{r} \frac{\partial F}{\partial \theta} \big) = r \sin \theta \cos \theta \sin \phi \frac{\partial F}{\partial r} - \sin^2 \theta \sin \phi \frac{\partial F}{\partial \theta}$

and

$z \frac{\partial F}{\partial y} = r \cos \theta \big( \sin \theta \sin \phi \frac{\partial F}{\partial r} + \frac{\cos \theta \sin \phi}{r} \frac{\partial F}{\partial \theta} + \frac{\cos \phi}{r \sin \theta} \frac{\partial F}{\partial \phi}\big)$

$= r \cos \theta \sin \theta \sin \phi \frac{\partial F}{\partial r} + \cos^2 \theta \sin \phi \frac{\partial F}{\partial \theta} + \frac{\cos \theta \cos \phi}{\sin \theta}\frac{\partial F}{\partial \phi}$

Subtracting the second expression from the first and ignoring the $F$ in the numerators of the partial derivatives we can then write the angular momentum operator in the $x-$ direction in terms of spherical polar coordinates as

$L_x = - i \hbar \big( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y} \big)$

$= - i \hbar \big( - \cot \theta \cos \phi \frac{\partial}{\partial \phi} - \sin \phi \frac{\partial}{\partial \theta} \big)$

$= i \hbar \big(\cot \theta \cos \phi \frac{\partial}{\partial \phi} + \sin \phi \frac{\partial}{\partial \theta} \big)$

Similarly we have

$z \frac{\partial F}{\partial x} = r \cos \theta \big( \sin \theta \cos \phi \frac{\partial F}{\partial r} + \frac{\cos \theta \cos \phi}{r} \frac{\partial F}{\partial \theta} - \frac{\sin \phi}{r \sin \theta} \frac{\partial F}{\partial \phi}\big)$

$= r \cos \theta \sin \theta \cos \phi \frac{\partial F}{\partial r} + \cos^2 \theta \cos \phi \frac{\partial F}{\partial \theta} - \frac{\cos \theta \sin \phi}{\sin \theta}\frac{\partial F}{\partial \phi}$

and

$x \frac{\partial F}{\partial z} = r \sin \theta \cos \phi \big( \cos \theta \frac{\partial F}{\partial r} - \frac{\sin \theta}{r} \frac{\partial F}{\partial \theta} \big) = r \sin \theta \cos \theta \cos \phi \frac{\partial F}{\partial r} - \sin^2 \theta \cos \phi \frac{\partial F}{\partial \theta}$

Therefore

$L_y = - i \hbar \big( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z} \big)$

$= - i \hbar \big(\cos \phi \frac{\partial}{\partial \theta} - \cot \theta \sin \phi \frac{\partial}{\partial \phi} \big)$

Finally, we have

$x \frac{\partial F}{\partial y} = r \sin \theta \cos \phi \big( \sin \theta \sin \phi \frac{\partial F}{\partial r} + \frac{\cos \theta \sin \phi}{r} \frac{\partial F}{\partial \theta} + \frac{\cos \phi}{r \sin \theta} \frac{\partial F}{\partial \phi}\big)$

$= r \sin^2 \theta \cos \phi \sin \phi \frac{\partial F}{\partial r} + \sin \theta \cos \theta \sin \phi \cos \phi \frac{\partial F}{\partial \theta} + \cos^2 \phi \frac{\partial F}{\partial \phi}$

and

$y \frac{\partial F}{\partial x} = r \sin \theta \sin \phi \big( \sin \theta \cos \phi \frac{\partial F}{\partial r} + \frac{\cos \theta \cos \phi}{r} \frac{\partial F}{\partial \theta} - \frac{\sin \phi}{r \sin \theta} \frac{\partial F}{\partial \phi}\big)$

$= r \sin^2 \theta \cos \phi \sin \phi \frac{\partial F}{\partial r} + \sin \theta \cos \theta \sin \phi \cos \phi \frac{\partial F}{\partial \theta} - \sin^2 \phi \frac{\partial F}{\partial \phi}$

Therefore

$L_z = - i \hbar \big( x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \big)$

$= - i \hbar \frac{\partial}{\partial \phi}$

Having obtained the components of $\mathbf{L}$ in spherical polar coordinates we can now finally calculate the operator representation of $L^2$ as

$L^2 = L_x^2 + L_y^2 + L_z^2$

$= \big[ i \hbar \big(\cot \theta \cos \phi \frac{\partial}{\partial \phi} + \sin \phi \frac{\partial}{\partial \theta} \big) \big]^2 + \big[ - i \hbar \big(\cos \phi \frac{\partial}{\partial \theta} - \cot \theta \sin \phi \frac{\partial}{\partial \phi} \big) \big]^2 + \big[ - i \hbar \frac{\partial}{\partial \phi} \big]^2$

$= - \hbar^2 \big[ \sin^2 \phi \frac{\partial^2}{\partial \theta^2} + \big(\sin \phi \frac{\partial}{\partial \theta} \big) \big(\cot \theta \cos \phi \frac{\partial}{\partial \phi} \big) + \big(\cot \theta \cos \phi \frac{\partial}{\partial \phi} \big)\big(\sin \phi \frac{\partial}{\partial \theta} \big) + \cot^2 \theta \cos^2 \phi \frac{\partial^2}{\partial \phi^2} \big]$

$- \hbar^2 \big[ \cos^2 \phi \frac{\partial^2}{\partial \theta^2} - \big(\cos \phi \frac{\partial}{\partial \theta} \big) \big(\cot \theta \sin \phi \frac{\partial}{\partial \phi} \big) - \big(\cot \theta \sin \phi \frac{\partial}{\partial \phi} \big)\big(\cos \phi \frac{\partial}{\partial \theta} \big) + \cot^2 \theta \sin^2 \phi \frac{\partial^2}{\partial \phi^2} \big]$

$- \hbar^2 \frac{\partial^2}{\partial \phi^2}$

$= - \hbar^2 \big( \frac{\partial^2}{\partial \theta^2} + \cot^2 \theta \frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \phi^2} - \sin \phi \frac{1}{\sin^2 \theta} \cos \phi \frac{\partial}{\partial \phi} + \cot \theta \cos^2 \phi \frac{\partial}{\partial \theta}$

$+ \cos \phi \frac{1}{\sin^2 \theta} \sin \phi \frac{\partial}{\partial \phi} + \cot \theta \sin^2 \phi \frac{\partial}{\partial \theta}\big)$

$= - \hbar^2 \big( \frac{\partial^2}{\partial \theta^2} + \cot \theta \frac{\partial}{\partial \theta} + \cot^2 \theta \frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \phi^2}\big)$

$= - \hbar^2 \big( \frac{1}{\sin \theta}\frac{\partial}{\partial \theta} \big( \sin \theta \frac{\partial}{\partial \theta}\big) + \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \phi^2} \big)$

Changing variables in the square of the angular momentum operator

Published by Dr Christian P. H. Salas

Leave a comment Cancel reply