Dirichlet character tables up to mod 11

Certain arithmetical functions, known as Dirichlet characters mod $k$ , are used extensively in analytic number theory. Given an arbitrary group $G$ , a character of $G$ is generally a complex-valued function $f$ with domain $G$ such that $f$ has the multiplicative property $f(ab) = f(a)f(b)$ for all $a, b \in G$ , and such that $f(c) \neq 0$ for some $c \in G$ . Dirichlet characters mod $k$ are certain characters defined for a particular type of group $G$ , namely the group of reduced residue classes modulo a fixed positive integer $k$ . A reduced residue system modulo $k$ is a set of $\varphi(k)$ integers

$\{a_1, a_2, \ldots, a_{\varphi(k)} \}$

which are incongruent modulo $k$ , and each of which is relatively prime to $k$ (the function $\varphi(k)$ is Euler’s totient function, which counts the number of positive integers not exceeding $k$ which are coprime with $k$ ). For each integer $a$ in this set, we define a residue class $[a]_k$ as the set of all integers which are congruent to $a$ modulo $k$ . For example, for $k = 12$ , we have $\varphi(12) = 4$ and one reduced residue system mod $12$ is $\{1, 5, 7, 11\}$ . The reduced residue classes mod $12$ are then

$[1]_{12} = \{1, 13, 25, \ldots\}$

$[5]_{12} = \{5, 17, 29, \ldots\}$

$[7]_{12} = \{7, 19, 31, \ldots\}$

$[11]_{12} = \{11, 23, 35, \ldots\}$

What we are saying is that this set $\{[1]_{12}, [5]_{12}, [7]_{12}, [11]_{12}\}$ of reduced residue classes mod $12$ form a group, and the Dirichlet characters mod $12$ are certain characters defined for this group. In general, if we define multiplication of residue classes by

$[a]_k \cdot [b]_k = [ab]_k$

(i.e., the product of the residue classes of $a$ and $b$ is the residue class of the product $ab$ ), then the set of reduced residue classes modulo $k$ forms a finite abelian group of order $\varphi(k)$ with this operation. The identity is the residue class $[1]_k$ . The inverse of $[a]_k$ in the group is the residue class $[b]_k$ such that $ab \equiv 1$ mod $k$ . If we let $G$ be the group of reduced residue classes mod $k$ , with characters $f$ , then we define the Dirichlet characters mod $k$ as arithmetical functions of the form

$\chi(n) = \left \{ \begin{array}{c c} f([n]_k) & \text{if } gcd(n, k) = 1\\ 0 & \ \text{if } gcd(n, k) > 1 \end{array} \right.$

There are $\varphi(k)$ distinct Dirichlet characters $\chi$ modulo $k$ , each of which is completely multiplicative and periodic with period $k$ . Each character value $\chi(n)$ is a (complex) root of unity if $gcd(n, k) = 1$ whereas $\chi(n) = 0$ whenever $gcd(n, k) > 1$ . We also have $\chi(1) = 1$ for all Dirichlet characters. For each $k$ , there is one character, called the principal character, which is such that

$\chi(n) = \left \{ \begin{array}{c c} 1 & \text{if } gcd(n, k) = 1\\ 0 & \ \text{if } gcd(n, k) > 1 \end{array} \right.$

These facts uniquely determine the Dirichlet character table for each $k$ . For reference purposes, I will set out the first ten Dirichlet character tables in the present note and demonstrate their calculation in detail.

k = 2

We have $\varphi(2) = 1$ so there is only one Dirichlet character in this case (the principal one), with values $\chi_1(1) = 1$ and $\chi_1(2) = 0$ .

k = 3

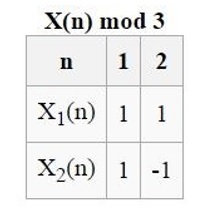
We have $\varphi(3) = 2$ so there are two Dirichlet characters in this case. One of them will be the principal character which takes the values $\chi_1(1) = 1$ , $\chi_1(2) = 1$ and $\chi_1(3) = 0$ . To work out the second Dirichlet character we consider the two roots of unity

$\omega = e^{2 \pi i/2} = e^{\pi i} = -1$

and

$\omega^2 = 1$

Note that the set of least positive residues mod $3$ is generated by $2$ :

$2 \equiv 2$ mod( $3$ )

$2^2 \equiv 1$ mod( $3$ )

Therefore the non-principal Dirichlet character will be completely determined by the values of $\chi(2)$ . If we set

$\chi_2(2) = \omega = -1$

then

$\chi_2(1) = \chi_2(2^2) = \chi_2^2(2) = \omega^2 = 1$

(though this calculation is superfluous here since $\chi_2(1) = 1$ anyway. This is a fundamental property of Dirichlet characters arising from the fact that they are completely multiplicative). We also have $\chi_2(3) = 0$ . This completes the second character. (From now on we will omit the statements of the zero values of the Dirichlet characters, which as stated earlier arise whenever $gcd(n, k) > 1$ ).

k = 4

We have $\varphi(4) = 2$ so there are two Dirichlet characters in this case. One of them will be the principal character. (From now on we will always denote the principal character by $\chi_1$ ). To work out the second Dirichlet character we again consider the two roots of unity

$\omega = e^{2 \pi i/2} = e^{\pi i} = -1$

and

$\omega^2 = 1$

Note that the set of least positive residues mod $4$ is generated by $3$ :

$3 \equiv 3$ mod( $4$ )

$3^2 \equiv 1$ mod( $4$ )

Therefore the non-principal Dirichlet character will be completely determined by the values of $\chi(3)$ . If we set

$\chi_2(3) = \omega = -1$

then

$\chi_2(1) = \chi_2(3^2) = \chi_2^2(3) = \omega^2 = 1$

(though again this second calculation is superfluous since $\chi_2(1) = 1$ anyway). This completes the second character.

k = 5

We have $\varphi(5) = 4$ so there are four Dirichlet characters in this case. We consider the four roots of unity

$\omega = e^{2 \pi i/4} = e^{\pi i/2} = i$

$\omega^2 = e^{4 \pi i/4} = e^{\pi i} = -1$

$\omega^3 = e^{6 \pi i/4} = e^{3 \pi i/2} = -i$

$\omega^4 = e^{8 \pi i/4} = e^{2 \pi i} = 1$

Note that the set of least positive residues mod $5$ is generated by $2$ :

$2 \equiv 2$ mod( $5$ )

$2^2 \equiv 4$ mod( $5$ )

$2^3 \equiv 3$ mod( $5$ )

$2^4 \equiv 1$ mod( $5$ )

Therefore the non-principal Dirichlet characters will be completely determined by the values of $\chi(2)$ . If we set

$\chi_2(2) = \omega = i$

then

$\chi_2(3) = \chi_2(2^3) = \chi_2^3(2) = -i$

$\chi_2(4) = \chi_2(2^2) = \chi_2^2(2) = -1$

(and we have $\chi_2(1) = 1$ ). This completes the second character.

To compute the third character we can set

$\chi_3(2) = \omega^2 = -1$

then

$\chi_3(3) = \chi_3(2^3) = \chi_3^3(2) = -1$

$\chi_3(4) = \chi_3(2^2) = \chi_3^2(2) = 1$

(and we have $\chi_3(1) = 1$ ). This completes the third character.

To compute the fourth character we set

$\chi_4(2) = \omega^3 = -i$

then

$\chi_4(3) = \chi_4(2^3) = \chi_4^3(2) = i$

$\chi_4(4) = \chi_4(2^2) = \chi_4^2(2) = -1$

(and we have $\chi_4(1) = 1$ ). This completes the fourth character.

k = 6

We have $\varphi(6) = 2$ so there are two Dirichlet characters in this case. We consider the two roots of unity

$\omega = e^{2 \pi i/2} = e^{\pi i} = -1$

and

$\omega^2 = 1$

Note that the set of least positive residues mod $6$ is generated by $5$ :

$5 \equiv 5$ mod( $6$ )

$5^2 \equiv 1$ mod( $6$ )

Therefore the non-principal Dirichlet character will be completely determined by the values of $\chi(5)$ . If we set

$\chi_2(5) = \omega = -1$

then

$\chi_2(1) = \chi_2(5^2) = \chi_2^2(5) = \omega^2 = 1$

(though again this second calculation is superfluous since $\chi_2(1) = 1$ anyway). This completes the second character.

k = 7

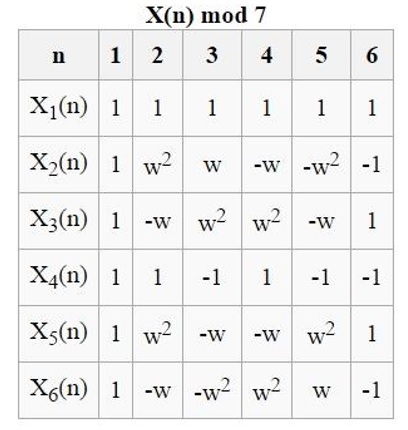
We have $\varphi(7) = 6$ so there are six Dirichlet characters in this case. We consider the six roots of unity

$\omega = e^{2 \pi i/6} = e^{\pi i/3}$

$\omega^2 = e^{2 \pi i/3}$

$\omega^3 = e^{3 \pi i/3} = e^{\pi i} = -1$

$\omega^4 = \omega \cdot \omega^3 = -\omega$

$\omega^5 = \omega \cdot \omega^4 = -\omega^2$

$\omega^6 = e^{6 \pi i/3} = e^{2\pi i} = 1$

Note that the set of least positive residues mod $7$ is generated by $3$ :

$3 \equiv 3$ mod( $7$ )

$3^2 \equiv 2$ mod( $7$ )

$3^3 \equiv 6$ mod( $7$ )

$3^4 \equiv 4$ mod( $7$ )

$3^5 \equiv 5$ mod( $7$ )

$3^6 \equiv 1$ mod( $7$ )

Therefore the non-principal Dirichlet characters will be completely determined by the values of $\chi(3)$ . If we set

$\chi_2(3) = \omega$

then

$\chi_2(2) = \chi_2(3^2) = \chi_2^2(3) = \omega^2$

$\chi_2(4) = \chi_2(3^4) = \chi_2^4(3) = \omega^4 = -\omega$

$\chi_2(5) = \chi_2(3^5) = \chi_2^5(3) = \omega^5 = -\omega^2$

$\chi_2(6) = \chi_2(3^3) = \chi_2^3(3) = \omega^3 = -1$

(and we have $\chi_2(1) = 1$ ). This completes the second character.

To compute the third character we can set

$\chi_3(3) = \omega^2$

then

$\chi_3(2) = \chi_3(3^2) = \chi_3^2(3) = \omega^4 = -\omega$

$\chi_3(4) = \chi_3(3^4) = \chi_3^4(3) = \omega^8 = \omega^2$

$\chi_3(5) = \chi_3(3^5) = \chi_3^5(3) = \omega^{10} = -\omega$

$\chi_3(6) = \chi_3(3^3) = \chi_3^3(3) = \omega^6 = 1$

(and we have $\chi_3(1) = 1$ ). This completes the third character.

To compute the fourth character we can set

$\chi_4(3) = \omega^3 = -1$

then

$\chi_4(2) = \chi_4(3^2) = \chi_4^2(3) = 1$

$\chi_4(4) = \chi_4(3^4) = \chi_4^4(3) = 1$

$\chi_4(5) = \chi_4(3^5) = \chi_4^5(3) = -1$

$\chi_4(6) = \chi_4(3^3) = \chi_4^3(3) = -1$

(and we have $\chi_4(1) = 1$ ). This completes the fourth character.

To compute the fifth character we can set

$\chi_5(3) = \omega^4 = -\omega$

then

$\chi_5(2) = \chi_5(3^2) = \chi_5^2(3) = \omega^2$

$\chi_5(4) = \chi_5(3^4) = \chi_5^4(3) = \omega^4 = -\omega$

$\chi_5(5) = \chi_5(3^5) = \chi_5^5(3) = \chi_5^4(3) \cdot \chi_5(3) = \omega^2$

$\chi_5(6) = \chi_5(3^3) = \chi_5^3(3) = -\omega^3 = 1$

(and we have $\chi_5(1) = 1$ ). This completes the fifth character.

Finally, to compute the sixth character we set

$\chi_6(3) = \omega^5 = -\omega^2$

then

$\chi_6(2) = \chi_6(3^2) = \chi_6^2(3) = \omega^4 = -\omega$

$\chi_6(4) = \chi_6(3^4) = \chi_6^4(3) = \omega^8 = \omega^2$

$\chi_6(5) = \chi_6(3^5) = \chi_6^5(3) = -\omega^{10} = \omega$

$\chi_6(6) = \chi_6(3^3) = \chi_6^3(3) = -\omega^6 = -1$

(and we have $\chi_6(1) = 1$ ). This completes the sixth character.

k = 8

We have $\varphi(8) = 4$ so there are four Dirichlet characters in this case. We consider the four roots of unity

$\omega = e^{2 \pi i/4} = e^{\pi i/2} = i$

$\omega^2 = e^{4 \pi i/4} = e^{\pi i} = -1$

$\omega^3 = e^{6 \pi i/4} = e^{3 \pi i/2} = -i$

$\omega^4 = e^{8 \pi i/4} = e^{2 \pi i} = 1$

In this case, none of the four elements of the set of least positive residues mod $8$ generates the entire set. However, the characters must satisfy the following relations, which restrict the choices:

$\chi(3) \cdot \chi(5) = \chi(15) = \chi(7)$

$\chi(3) \cdot \chi(7) = \chi(21) = \chi(5)$

$\chi(5) \cdot \chi(7) = \chi(35) = \chi(3)$

Each character’s values must be chosen in such a way that these three relations hold.

To compute the second character, suppose we begin by trying to set

$\chi_2(3) = \omega = i$

and

$\chi_2(5) = \omega^2 = -1$

Then we must have

$\chi_2(7) = \chi_2(3) \cdot \chi_2(5) = -i$

but then

$\chi_2(3) \cdot \chi_2(7) = 1 \neq \chi_2(5)$

so this does not work. If instead we try to set

$\chi_2(5) = -i$

then we must have

$\chi_2(7) = \chi_2(3) \cdot \chi_2(5) = 1$

but then

$\chi_2(3) \cdot \chi_2(7) = i \neq \chi_2(5)$

so this does not work either. Computations like these show that $\pm i$ cannot appear in any of the characters mod $8$ . All the characters must be formed from $\pm 1$ . (Fundamentally, this is due to the fact that the group of least positive residues mod $8$ can be subdivided into four cyclic subgroups of order 2, each of which has characters whose values are the two roots of unity, $1$ and $-1$ ).

To compute the second character we can set

$\chi_2(3) = 1$

and

$\chi_2(5) = -1$

then we must have

$\chi_2(7) = -1$

and this works.

To compute the third character we can set

$\chi_3(3) = -1$

and

$\chi_3(5) = -1$

then we must have

$\chi_3(7) = 1$

and this works too.

Finally, to compute the fourth character we can set

$\chi_4(3) = -1$

and

$\chi_4(5) = 1$

then we must have

$\chi_4(7) = -1$

and this works too.

k = 9

We have $\varphi(9) = 6$ so there are six Dirichlet characters in this case. We consider the six roots of unity

$\omega = e^{2 \pi i/6} = e^{\pi i/3}$

$\omega^2 = e^{2 \pi i/3}$

$\omega^3 = e^{3 \pi i/3} = e^{\pi i} = -1$

$\omega^4 = \omega \cdot \omega^3 = -\omega$

$\omega^5 = \omega \cdot \omega^4 = -\omega^2$

$\omega^6 = e^{6 \pi i/3} = e^{2\pi i} = 1$

Note that the set of least positive residues mod $9$ is generated by $2$ :

$2 \equiv 2$ mod( $9$ )

$2^2 \equiv 4$ mod( $9$ )

$2^3 \equiv 8$ mod( $9$ )

$2^4 \equiv 7$ mod( $9$ )

$2^5 \equiv 5$ mod( $9$ )

$2^6 \equiv 1$ mod( $9$ )

Therefore the non-principal Dirichlet characters will be completely determined by the values of $\chi(2)$ . If we set

$\chi_2(2) = \omega$

then

$\chi_2(4) = \chi_2(2^2) = \chi_2^2(2) = \omega^2$

$\chi_2(5) = \chi_2(2^5) = \chi_2^5(2) = \omega^5 = -\omega^2$

$\chi_2(7) = \chi_2(2^4) = \chi_2^4(2) = \omega^4 = -\omega$

$\chi_2(8) = \chi_2(2^3) = \chi_2^3(2) = \omega^3 = -1$

(and we have $\chi_2(1) = 1$ ). This completes the second character.

To compute the third character we can set

$\chi_3(2) = \omega^2$

then

$\chi_3(4) = \chi_3(2^2) = \chi_3^2(2) = \omega^4 = -\omega$

$\chi_3(5) = \chi_3(2^5) = \chi_3^5(2) = \omega^{10} = \omega^6 \cdot \omega^4 = -\omega$

$\chi_3(7) = \chi_3(2^4) = \chi_3^4(2) = \omega^8 = \omega^6 \cdot \omega^2 = \omega^2$

$\chi_3(8) = \chi_3(2^3) = \chi_3^3(2) = \omega^6 = 1$

(and we have $\chi_3(1) = 1$ ). This completes the third character.

To compute the fourth character we can set

$\chi_4(2) = \omega^3 = -1$

then

$\chi_4(4) = \chi_4(2^2) = \chi_4^2(2) = 1$

$\chi_4(5) = \chi_4(2^5) = \chi_4^5(2) = -1$

$\chi_4(7) = \chi_4(2^4) = \chi_4^4(2) = 1$

$\chi_4(8) = \chi_4(2^3) = \chi_4^3(2) = -1$

(and we have $\chi_4(1) = 1$ ). This completes the fourth character.

To compute the fifth character we can set

$\chi_5(2) = \omega^4 = -\omega$

then

$\chi_5(4) = \chi_5(2^2) = \chi_5^2(2) = \omega^2$

$\chi_5(5) = \chi_5(2^5) = \chi_5^5(2) = -\omega^5 = -\omega^3 \cdot \omega^2 = \omega^2$

$\chi_5(7) = \chi_5(2^4) = \chi_5^4(2) = \omega^4 = \omega^3 \cdot \omega = -\omega$

$\chi_5(8) = \chi_5(2^3) = \chi_5^3(2) = -\omega^3 = 1$

(and we have $\chi_5(1) = 1$ ). This completes the fifth character.

Finally, to compute the sixth character we can set

$\chi_6(2) = \omega^5 = -\omega^2$

then

$\chi_6(4) = \chi_6(2^2) = \chi_6^2(2) = \omega^4 = -\omega$

$\chi_6(5) = \chi_6(2^5) = \chi_6^5(2) = -\omega^{10} = -\omega^6 \cdot \omega^4 = \omega$

$\chi_6(7) = \chi_6(2^4) = \chi_6^4(2) = \omega^8 = \omega^6 \cdot \omega^2 = \omega^2$

$\chi_6(8) = \chi_6(2^3) = \chi_6^3(2) = -\omega^6 = -1$

(and we have $\chi_6(1) = 1$ ). This completes the sixth character.

k = 10

We have $\varphi(10) = 4$ so there are four Dirichlet characters in this case. We consider the four roots of unity

$\omega = e^{2 \pi i/4} = e^{\pi i/2} = i$

$\omega^2 = e^{4 \pi i/4} = e^{\pi i} = -1$

$\omega^3 = e^{6 \pi i/4} = e^{3 \pi i/2} = -i$

$\omega^4 = e^{8 \pi i/4} = e^{2 \pi i} = 1$

Note that the set of least positive residues mod $10$ is generated by $3$ :

$3 \equiv 3$ mod( $10$ )

$3^2 \equiv 9$ mod( $10$ )

$3^3 \equiv 7$ mod( $10$ )

$3^4 \equiv 1$ mod( $10$ )

Therefore the non-principal Dirichlet characters will be completely determined by the values of $\chi(3)$ . If we set

$\chi_2(3) = \omega = i$

then

$\chi_2(7) = \chi_2(3^3) = \chi_2^3(3) = -i$

$\chi_2(9) = \chi_2(3^2) = \chi_2^2(3) = -1$

(and we have $\chi_2(1) = 1$ ). This completes the second character.

To compute the third character we can set

$\chi_3(3) = \omega^2 = -1$

then

$\chi_3(7) = \chi_3(3^3) = \chi_3^3(3) = -1$

$\chi_3(9) = \chi_3(3^2) = \chi_3^2(3) = 1$

(and we have $\chi_3(1) = 1$ ). This completes the third character.

Finally, to compute the fourth character we set

$\chi_4(3) = \omega^3 = -i$

then

$\chi_4(7) = \chi_4(3^3) = \chi_4^3(3) = i$

$\chi_4(9) = \chi_4(3^2) = \chi_4^2(3) = -1$

(and we have $\chi_4(1) = 1$ ). This completes the fourth character.

k = 11

We have $\varphi(11) = 10$ so there are ten Dirichlet characters in this case. We consider the ten roots of unity

$\omega = e^{2 \pi i/10} = e^{\pi i/5}$

$\omega^2 = e^{2 \pi i/5}$

$\omega^3 = e^{3 \pi i/5}$

$\omega^4 = e^{4 \pi i/5}$

$\omega^5 = e^{5 \pi i/5} = e^{\pi i} = -1$

$\omega^6 = -\omega$

$\omega^7 = -\omega^2$

$\omega^8 = -\omega^3$

$\omega^9 = -\omega^4$

$\omega^{10} = -\omega^5 = 1$

Note that the set of least positive residues mod $11$ is generated by $2$ :

$2 \equiv 2$ mod( $11$ )

$2^2 \equiv 4$ mod( $11$ )

$2^3 \equiv 8$ mod( $11$ )

$2^4 \equiv 5$ mod( $11$ )

$2^5 \equiv 10$ mod( $11$ )

$2^6 \equiv 9$ mod( $11$ )

$2^7 \equiv 7$ mod( $11$ )

$2^8 \equiv 3$ mod( $11$ )

$2^9 \equiv 6$ mod( $11$ )

$2^{10} \equiv 1$ mod( $11$ )

Therefore the non-principal Dirichlet characters will be completely determined by the values of $\chi(2)$ . If we set

$\chi_2(2) = \omega$

then

$\chi_2(3) = \chi_2(2^8) = \chi_2^8(2) = \omega^8 = -\omega^3$

$\chi_2(4) = \chi_2(2^2) = \chi_2^2(2) = \omega^2$

$\chi_2(5) = \chi_2(2^4) = \chi_2^4(2) = \omega^4$

$\chi_2(6) = \chi_2(2^9) = \chi_2^9(2) = \omega^9 = -\omega^4$

$\chi_2(7) = \chi_2(2^7) = \chi_2^7(2) = \omega^7 = -\omega^2$

$\chi_2(8) = \chi_2(2^3) = \chi_2^3(2) = \omega^3$

$\chi_2(9) = \chi_2(2^6) = \chi_2^6(2) = \omega^6 = -\omega$

$\chi_2(10) = \chi_2(2^5) = \chi_2^5(2) = \omega^5 = -1$

(and we have $\chi_2(1) = 1$ ). This completes the second character.

To compute the third character we can set

$\chi_3(2) = \omega^2$

then

$\chi_3(3) = \chi_3(2^8) = \chi_3^8(2) = \omega^{16} = -\omega$

$\chi_3(4) = \chi_3(2^2) = \chi_3^2(2) = \omega^4$

$\chi_3(5) = \chi_3(2^4) = \chi_3^4(2) = \omega^8 = -\omega^3$

$\chi_3(6) = \chi_3(2^9) = \chi_3^9(2) = \omega^{18} = -\omega^3$

$\chi_3(7) = \chi_3(2^7) = \chi_3^7(2) = \omega^{14} = \omega^4$

$\chi_3(8) = \chi_3(2^3) = \chi_3^3(2) = \omega^6 = -\omega$

$\chi_3(9) = \chi_3(2^6) = \chi_3^6(2) = \omega^{12} = \omega^2$

$\chi_3(10) = \chi_3(2^5) = \chi_3^5(2) = \omega^{10} = 1$

(and we have $\chi_3(1) = 1$ ). This completes the third character.

To compute the fourth character we can set

$\chi_4(2) = \omega^3$

then

$\chi_4(3) = \chi_4(2^8) = \chi_4^8(2) = \omega^{24} = \omega^4$

$\chi_4(4) = \chi_4(2^2) = \chi_4^2(2) = \omega^6 = -\omega$

$\chi_4(5) = \chi_4(2^4) = \chi_4^4(2) = \omega^{12} = \omega^2$

$\chi_4(6) = \chi_4(2^9) = \chi_4^9(2) = \omega^{27} = -\omega^2$

$\chi_4(7) = \chi_4(2^7) = \chi_4^7(2) = \omega^{21} = \omega$

$\chi_4(8) = \chi_4(2^3) = \chi_4^3(2) = \omega^9 = -\omega^4$

$\chi_4(9) = \chi_4(2^6) = \chi_4^6(2) = \omega^{18} = -\omega^3$

$\chi_4(10) = \chi_4(2^5) = \chi_4^5(2) = \omega^{15} = -1$

(and we have $\chi_4(1) = 1$ ). This completes the fourth character.

To compute the fifth character we can set

$\chi_5(2) = \omega^4$

then

$\chi_5(3) = \chi_5(2^8) = \chi_5^8(2) = \omega^{32} = \omega^2$

$\chi_5(4) = \chi_5(2^2) = \chi_5^2(2) = \omega^8 = -\omega^3$

$\chi_5(5) = \chi_5(2^4) = \chi_5^4(2) = \omega^{16} = -\omega$

$\chi_5(6) = \chi_5(2^9) = \chi_5^9(2) = \omega^{36} = -\omega$

$\chi_5(7) = \chi_5(2^7) = \chi_5^7(2) = \omega^{28} = -\omega^3$

$\chi_5(8) = \chi_5(2^3) = \chi_5^3(2) = \omega^{12} = \omega^2$

$\chi_5(9) = \chi_5(2^6) = \chi_5^6(2) = \omega^{24} = \omega^4$

$\chi_5(10) = \chi_5(2^5) = \chi_5^5(2) = \omega^{20} = 1$

(and we have $\chi_5(1) = 1$ ). This completes the fifth character.

To compute the sixth character we can set

$\chi_6(2) = \omega^5 = -1$

then

$\chi_6(3) = \chi_6(2^8) = \chi_6^8(2) = 1$

$\chi_6(4) = \chi_6(2^2) = \chi_6^2(2) = 1$

$\chi_6(5) = \chi_6(2^4) = \chi_6^4(2) = 1$

$\chi_6(6) = \chi_6(2^9) = \chi_6^9(2) = -1$

$\chi_6(7) = \chi_6(2^7) = \chi_6^7(2) = -1$

$\chi_6(8) = \chi_6(2^3) = \chi_6^3(2) = -1$

$\chi_6(9) = \chi_6(2^6) = \chi_6^6(2) = 1$

$\chi_6(10) = \chi_6(2^5) = \chi_6^5(2) = -1$

(and we have $\chi_6(1) = 1$ ). This completes the sixth character.

To compute the seventh character we can set

$\chi_7(2) = \omega^6 = -\omega$

then

$\chi_7(3) = \chi_7(2^8) = \chi_7^8(2) = \omega^8 = -\omega^3$

$\chi_7(4) = \chi_7(2^2) = \chi_7^2(2) = \omega^2$

$\chi_7(5) = \chi_7(2^4) = \chi_7^4(2) = \omega^4$

$\chi_7(6) = \chi_7(2^9) = \chi_7^9(2) = -\omega^9 = \omega^4$

$\chi_7(7) = \chi_7(2^7) = \chi_7^7(2) = -\omega^7 = \omega^2$

$\chi_7(8) = \chi_7(2^3) = \chi_7^3(2) = -\omega^3$

$\chi_7(9) = \chi_7(2^6) = \chi_7^6(2) = \omega^6 = -\omega$

$\chi_7(10) = \chi_7(2^5) = \chi_7^5(2) = -\omega^5 = 1$

(and we have $\chi_7(1) = 1$ ). This completes the seventh character.

To compute the eighth character we can set

$\chi_8(2) = \omega^7 = -\omega^2$

then

$\chi_8(3) = \chi_8(2^8) = \chi_8^8(2) = \omega^{16} = -\omega$

$\chi_8(4) = \chi_8(2^2) = \chi_8^2(2) = \omega^4$

$\chi_8(5) = \chi_8(2^4) = \chi_8^4(2) = \omega^8 = -\omega^3$

$\chi_8(6) = \chi_8(2^9) = \chi_8^9(2) = -\omega^{18} = \omega^3$

$\chi_8(7) = \chi_8(2^7) = \chi_8^7(2) = -\omega^{14} = -\omega^4$

$\chi_8(8) = \chi_8(2^3) = \chi_8^3(2) = -\omega^6 = \omega$

$\chi_8(9) = \chi_8(2^6) = \chi_8^6(2) = \omega^{12} = \omega^2$

$\chi_8(10) = \chi_8(2^5) = \chi_8^5(2) = -\omega^{10} = -1$

(and we have $\chi_8(1) = 1$ ). This completes the eighth character.

To compute the ninth character we can set

$\chi_9(2) = \omega^8 = -\omega^3$

then

$\chi_9(3) = \chi_9(2^8) = \chi_9^8(2) = \omega^{24} = \omega^4$

$\chi_9(4) = \chi_9(2^2) = \chi_9^2(2) = \omega^6 = -\omega$

$\chi_9(5) = \chi_9(2^4) = \chi_9^4(2) = \omega^{12} = \omega^2$

$\chi_9(6) = \chi_9(2^9) = \chi_9^9(2) = -\omega^{27} = \omega^2$

$\chi_9(7) = \chi_9(2^7) = \chi_9^7(2) = -\omega^{21} = -\omega$

$\chi_9(8) = \chi_9(2^3) = \chi_9^3(2) = -\omega^9 = \omega^4$

$\chi_9(9) = \chi_9(2^6) = \chi_9^6(2) = \omega^{18} = -\omega^3$

$\chi_9(10) = \chi_9(2^5) = \chi_9^5(2) = -\omega^{15} = 1$

(and we have $\chi_9(1) = 1$ ). This completes the ninth character.

Finally, to compute the tenth character we set

$\chi_{10}(2) = \omega^9 = -\omega^4$

then

$\chi_{10}(3) = \chi_{10}(2^8) = \chi_{10}^8(2) = \omega^{32} = \omega^2$

$\chi_{10}(4) = \chi_{10}(2^2) = \chi_{10}^2(2) = \omega^8 = -\omega^3$

$\chi_{10}(5) = \chi_{10}(2^4) = \chi_{10}^4(2) = \omega^{16} = -\omega$

$\chi_{10}(6) = \chi_{10}(2^9) = \chi_{10}^9(2) = -\omega^{36} = \omega$

$\chi_{10}(7) = \chi_{10}(2^7) = \chi_{10}^7(2) = -\omega^{28} = \omega^3$

$\chi_{10}(8) = \chi_{10}(2^3) = \chi_{10}^3(2) = -\omega^{12} = -\omega^2$

$\chi_{10}(9) = \chi_{10}(2^6) = \chi_{10}^6(2) = \omega^{24} = \omega^4$

$\chi_{10}(10) = \chi_{10}(2^5) = \chi_{10}^5(2) = -\omega^{20} = -1$

(and we have $\chi_{10}(1) = 1$ ). This completes the tenth character.

Dirichlet character tables up to mod 11

Published by Dr Christian P. H. Salas

Leave a comment Cancel reply