Monomer injections leading to oscillatory behaviour in a mathematical model of rain formation

In a previous note, I outlined a mathematical model of rapid-onset rain formation published by Michael Wilkinson in Physical Review Letters, which will be referred to as MW2016 herein. (Full reference: Wilkinson, M., 2016, Large Deviation Analysis of Rapid Onset of Rain Showers, Phys. Rev. Lett. 116, 018501). In the present note, I want to briefly record an interesting experiment in which I augmented the framework in MW2016 by allowing monomer injections to oppose the reduction in the volume fraction of liquid water content due to runaway collisions in equation [11] in MW2016. I show that this immediately leads to the possibility of oscillatory behaviour in Wilkinson’s model.

The simplest possible assumption is that of a constant monomer injection rate which increases the volume fraction at a constant rate $\alpha$ , thus changing the differential equation presented as equation [11] in MW2016 to

$\frac{d \Phi_l}{d t} = \alpha - \mathcal{N} \Phi_l P(t) \qquad \qquad \qquad \qquad \qquad (1)$

For convenience we will write

$\bar{\mathcal{N}} \equiv \mathcal{N} P(t) \qquad \qquad \qquad \qquad \qquad (2)$

so that (1) becomes

$\frac{d \Phi_l}{d t} = \alpha - \bar{\mathcal{N}} \Phi_l \qquad \qquad \qquad \qquad \qquad (3)$

This addition of monomer injections to equation [11] in MW2016 immediately gives rise to the possibility of oscillatory behaviour in the collector drop model because $\bar{\mathcal{N}}$ also depends on the volume fraction $\Phi_l$ , so there is a feedback loop between them. Suppose we capture this dependence by postulating that the fractional change in the number of collisions $\bar{\mathcal{N}}$ is related to the liquid content volume fraction $\Phi_l$ via some unknown function $g$ , so that

$\frac{1}{\bar{\mathcal{N}}} \frac{d \bar{\mathcal{N}}}{d t} = g(\Phi_l) \qquad \qquad \qquad \qquad \qquad (4)$

A Maclaurin series approximation of the unknown function $g$ to second order gives

$g(\Phi_l) = g(0) + g^{\prime}(0) \Phi_l + \frac{1}{2}g^{\prime \prime}(0) \Phi_l^2 \qquad \qquad \qquad \qquad \qquad (5)$

and putting this into (4) gives

$\frac{d \bar{\mathcal{N}}}{d t} = g(0)\bar{\mathcal{N}} + g^{\prime}(0) \bar{\mathcal{N}} \Phi_l + \frac{1}{2}g^{\prime \prime}(0) \bar{\mathcal{N}} \Phi_l^2 \qquad \qquad \qquad \qquad \qquad (6)$

Equations (3) and (6) now form a coupled ODE system reminiscent of a Lotka-Volterra system, and this is capable of yielding oscillatory behaviour in both the number of collisions $\bar{\mathcal{N}}$ and the volume fraction $\Phi_l$ , depending on the parameters $\alpha$ , $g(0)$ , $g^{\prime}(0)$ and $g^{\prime \prime}(0)$ . In fact, numerical experiments with (3) and (6) show that the numbers of collisions $\bar{\mathcal{N}}$ in particular can oscillate violently in the initial stages of the interaction, before adjustment to equilibrium eventually takes place. In all numerical experiments in which oscillations are observed, the amplitudes of the oscillations in $\bar{\mathcal{N}}$ are highest when the value of the time variable is small, becoming damped as the value of the time variable increases.

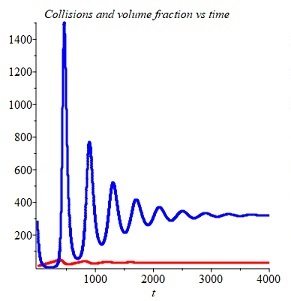
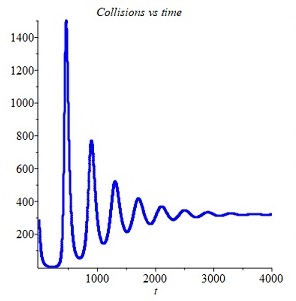
The above figures show classic damped oscillation patterns obtained in one such computation, carried out using MAPLE, with scaled variables representing the number of collisions divided by $10^3$ , and the volume fraction multiplied by $10^8$ (due to the very large difference in magnitude between $\bar{\mathcal{N}}$ and $\Phi_l$ ), with $\alpha = 0.1$ , $g(0) = -0.00004$ , $g^{\prime}(0) = 4$ and $g^{\prime \prime}(0) = 400,000,000$ . (As a check, identical results were obtained using MATLAB and FORTRAN. See the screenshots below).

The observation that oscillatory behaviour arises so easily after incorporation of monomer injections into the model, due to the resulting Lotka-Volterra type of interaction between $\bar{\mathcal{N}}$ and $\Phi_l$ , might have some connection to the oscillatory behaviour reported in previous work on coagulation systems driven by monomer inputs and large cluster outputs (e.g., Ball, R., Connaughton, C., Jones, P., Rajesh, R., Zaboronski, O., 2012, Collective Oscillations in Irreversible Coagulation Driven by Monomer Inputs and Large-Cluster Outputs, Phys. Rev. Lett. 109, 168304). Further investigation would be needed to clarify this.

The following are screenshots of the MAPLE, MATLAB and FORTRAN programs I used to carry out these experiments.

MAPLE: