Fast Fourier Transform by hand

I record here an experience of manually calculating a Fast Fourier Transform (FFT). Carrying out the computations by hand turned out to be relatively straightforward and quite instructive. A number of different FFT algorithms have been developed and the underlying equations are provided in numerous journal articles and books. I chose to calculate an eight-point (real-valued) FFT using the equations and approach discussed in the book Approximation Theory and Methods by M. J. D. Powell.

The classical Fourier analysis problem is to express a periodic function $f(x)$ of period $2\pi$ in the form

$f(x) = \frac{1}{2}a_0 + a_1 \cos(x) + a_2 \cos(2x) + \cdots + b_1 \sin(x) + b_2 \sin(2x) + \cdots$

In the context of approximation theory, the above Fourier series is truncated so that some $n > 0$ is the highest value of $j$ for which at least one of $a_j$ or $b_j$ is non-zero, i.e.,

$q(x) = \frac{1}{2}a_0 + \sum_{j=1}^n\big[a_j \cos(jx) + b_j \sin(jx) \big]$

We then regard $q(x)$ as a trigonometric polynomial of degree $n$ which approximates the function $f(x)$ (this approximation can be shown to minimise a least squares distance function).

The task is to find formulas for the coefficients $a_j$ and $b_j$ and this is achieved using the following formulas for the average values over a period of $\sin(jx) \cos(jx)$ , $\sin(jx) \sin(kx)$ and $\cos(jx) \cos(kx)$ respectively:

$\frac{1}{2 \pi} \int_{-\pi}^{\pi} \sin(jx) \cos(jx) dx = 0$

$\frac{1}{2 \pi} \int_{-\pi}^{\pi} \sin(jx) \sin(kx) dx = \begin{cases} 0 & j \neq k \\ \frac{1}{2} & j = k \neq 0 \\ 0 & j = k = 0 \end{cases}$

$\frac{1}{2 \pi} \int_{-\pi}^{\pi} \cos(jx) \cos(kx) dx= \begin{cases} 0 & j \neq k \\ \frac{1}{2} & j = k \neq 0 \\ 1 & j = k = 0 \end{cases}$

Then to find the value of the coefficient $a_0$ in the Fourier series expansion of $f(x)$ we take the average value of the series by integrating on $(-\pi, \pi)$ term by term. We get

$\frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx = \frac{1}{2 \pi} \int_{-\pi}^{\pi} \frac{1}{2} a_0 dx$

with all the other terms on the right-hand side equal to zero because they can all be regarded as integrals of $\sin(kx) \cos(jx)$ or of $\cos(jx) \cos(kx)$ with $j = 0$ and $k \neq 0$ (i.e., $j \neq k$ ). We are thus left with

$a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) dx$

This is the formula for calculating the coefficient $a_0$ in the Fourier series expansion of a periodic function $f(x)$ . From then on, to find $a_j$ for $j \neq 0$ , we multiply both sides of the generic Fourier series expansion by $\cos(jx)$ and again find the average value of each term to get

$a_j = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(jx) dx$

Analogously, to obtain the formula for $b_j$ , we multiply both sides of the generic Fourier series expansion by $\sin(jx)$ and take average values. We find

$b_j = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(jx) dx$

This classical setup assumes that the values of the function $f(x)$ are known for all $x$ in the interval $[-\pi, \pi]$ . When this is not the case and we only have the values of $f(x)$ for a discrete set of points in the interval $[-\pi, \pi]$ , we need to use a discretised form of Fourier series approximation. Powell approaches this in Section 13.3 of his book as follows:

Therefore the classical formulas

$a_j = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(jx) dx$

and

$b_j = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(jx) dx$

are replaced by formulas (13.36) and (13.37) in the excerpt above. To illustrate how these formulas work in a concrete example, suppose the problem is to to obtain an approximation of a function $f(x)$ by a trigonometric polynomial of degree $2$ given only the four function values $f(0) = 0.2$ , $f(\pi/2) = 0.25$ , $f(\pi) = 1.0$ and $f(3\pi/2) = 0.5$ . Thus, we need to obtain an approximation to $f$ of the form

$q(x) = \frac{1}{2}a_0 + \sum_{j=1}^2\big[a_j \cos(jx) + b_j \sin(jx) \big]$

Setting $N = 4$ , we use formulas (13.36) and (13.37) to evaluate the coefficients $a_0$ , $a_1$ , $a_2$ , $b_1$ and $b_2$ as follows:

$a_0 = \frac{2}{N} \sum_{k=0}^{N-1} f\big(\frac{2\pi k}{N}\big) \cos\big(\frac{2\pi j k}{N}\big)$

$= \frac{2}{4} \big[f(0)\cos(0) + f\big(\frac{2\pi}{4}\big) + f\big(\frac{4\pi}{4}\big) + f\big(\frac{6\pi}{4}\big)\big] = 0.975$

$a_1 = \frac{2}{4} \big[f(0)\cos(0) + f\big(\frac{2\pi}{4}\big)\cos\big(\frac{2\pi}{4}\big) + f\big(\frac{4\pi}{4}\big)\cos\big(\frac{4\pi}{4}\big) + f\big(\frac{6\pi}{4}\big)\cos\big(\frac{6\pi}{4}\big)\big] = -0.4$

$a_2 = \frac{2}{4} \big[f(0)\cos(0) + f\big(\frac{2\pi}{4}\big)\cos\big(\frac{4\pi}{4}\big) + f\big(\frac{4\pi}{4}\big)\cos\big(\frac{8\pi}{4}\big) + f\big(\frac{6\pi}{4}\big)\cos\big(\frac{12\pi}{4}\big)\big] = 0.225$

$b_1 = \frac{2}{N} \sum_{k=0}^{N-1} f\big(\frac{2\pi k}{N}\big) \sin\big(\frac{2\pi j k}{N}\big)$

$= \frac{2}{4} \big[f(0)\sin(0) + f\big(\frac{2\pi}{4}\big)\sin\big(\frac{2\pi}{4}\big) + f\big(\frac{4\pi}{4}\big)\sin\big(\frac{4\pi}{4}\big) + f\big(\frac{6\pi}{4}\big)\sin\big(\frac{6\pi}{4}\big)\big] = -0.125$

$b_2 = \frac{2}{4} \big[f(0)\sin(0) + f\big(\frac{2\pi}{4}\big)\sin\big(\frac{4\pi}{4}\big) + f\big(\frac{4\pi}{4}\big)\sin\big(\frac{8\pi}{4}\big) + f\big(\frac{6\pi}{4}\big)\sin\big(\frac{12\pi}{4}\big)\big] = 0$

Therefore the required approximation is

$q(x) = 0.4875 - 0.4 \cos(x) - 0.125 \sin(x) + 0.225 \cos(2x) + 0 \sin(2x)$

The fast Fourier transform is designed to speed up the calculations in discrete Fourier series approximations of the above kind in cases when $N$ is large. Powell discusses this in Section 13.4 of his book as follows:

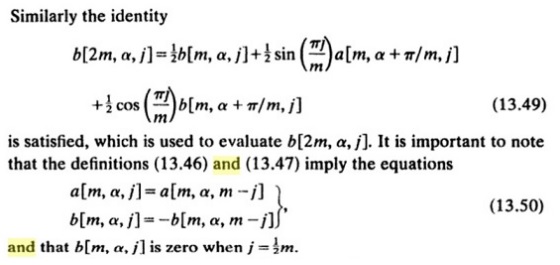
Each iteration of the FFT process depends on the value of the iteration variable $m$ , which initially is set at 1. In each subsequent iteration, the value of $m$ is set at twice the previous value, so in the second iteration we have $m = 2$ , in the third iteration we have $m = 4$ , in the fourth iteration we have $m = 8$ and so on. This continues until the value of the iteration variable reaches $N$ (which in this particular FFT approach is required to be a power of $2$ ).

At the start of the first iteration we set $m = 1$ and $j = 0$ . Formula (13.46) then reduces to

$a[1, \alpha, 0] = 2f(\alpha)$

and formula (13.47) reduces to

$b[1, \alpha, 0] = 0$

where for each $m$ the values of $\alpha$ are the numbers in the set

$\big\{\frac{2\pi k}{N}: k = 0, 1, \ldots, \frac{N}{m}-1\big\}$

So, in the first iteration we use the above formulas to generate $N$ values of $a[1, \alpha, 0]$ and $b[1, \alpha, 0]$ . We then use formulas (13.50) to obtain the numbers $a[1, \alpha, 1]$ and $b[1, \alpha, 1]$ . We get

$a[1, \alpha, 1] = a[1, \alpha, 0] = 2f(\alpha)$

$b[1, \alpha, 1] = -b[1, \alpha, 0] = 0$

Thus, the numbers $a[1, \alpha, 1]$ and $b[1, \alpha, 1]$ are exactly the same as the numbers $a[1, \alpha, 0]$ and $b[1, \alpha, 0]$ in this first iteration. At this point we are ready to begin the second iteration.

For the second iteration we double the iteration variable and use the results from the first iteration to compute the numbers $a[2, \alpha, j]$ and $b[2, \alpha, j]$ for $j = 0, 1$ using formulas (13.48) and (13.49). The variable $k$ runs from $0$ to $\frac{N}{2} - 1$ in this second iteration. We then use formulas (13.50) to obtain the numbers $a[2, \alpha, j]$ and $b[2, \alpha, j]$ for $j = 2$ and at this point we are ready to begin the third iteration.

For the third iteration we double the iteration variable again (so $m = 4$ ) and use the results from the second iteration to compute the numbers $a[4, \alpha, j]$ and $b[4, \alpha, j]$ for $j = 0, 1, 2$ using formulas (13.48) and (13.49). The variable $k$ runs from $0$ to $\frac{N}{4} - 1$ in this third iteration. We then use formulas (13.50) to obtain the numbers $a[4, \alpha, j]$ and $b[4, \alpha, j]$ for $j = 3, 4$ and at this point we are ready to begin the fourth iteration.

For the fourth iteration we double the iteration variable again (so $m = 8$ ) and use the results from the third iteration to compute the numbers $a[8, \alpha, j]$ and $b[8, \alpha, j]$ for $j = 0, 1, 2, 3, 4$ using formulas (13.48) and (13.49). The variable $k$ runs from $0$ to $\frac{N}{8} - 1$ in this fourth iteration. We then use formulas (13.50) to obtain the numbers $a[8, \alpha, j]$ and $b[8, \alpha, j]$ for $j = 5, 6, 7, 8$ and at this point we are ready to begin the fifth iteration.

Thus, we see that at the end of each iteration the numbers $a[m, \alpha, j]$ and $b[m, \alpha, j]$ are known, where $j$ takes all the integer values in $[0, m]$ and the variable $k$ runs from $0$ to $\frac{N}{m}-1$ . The iterations continue in this fashion until we arrive at the numbers $a_j = a[N, 0, j]$ and $b_j = b[N, 0, j]$ for $j = 0, 1, 2, \ldots, \frac{1}{2}N + 1$ and these provide the required coefficients for the approximation.

To illustrate how all of this works in a concrete example, I will solve a problem at the end of this chapter of Powell’s book. The problem reads as follows:

Therefore, we need to obtain an approximation to the data of the form

$q(x) = \frac{1}{2}a_0 + \sum_{j=1}^3\big[a_j \cos(jx) + b_j \sin(jx) \big]$

Applying the iterative process described above with $N = 8$ , we begin by setting $m = 1$ , $j = 0$ and $k = 0, 1, \ldots, 7$ in formulas (13.46) and (13.47). Formula (13.46) reduces to

$a[1, \alpha, 0] = 2f(\alpha)$

so we get the eight values

$a\big[1, \frac{2\pi \cdot 0}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 0}{8}\big) = -0.224356$

$a\big[1, \frac{2\pi \cdot 1}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 1}{8}\big) = 2.159318$

$a\big[1, \frac{2\pi \cdot 2}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 2}{8}\big) = 4.345334$

$a\big[1, \frac{2\pi \cdot 3}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 3}{8}\big) = 0.753214$

$a\big[1, \frac{2\pi \cdot 4}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 4}{8}\big) = -0.642824$

$a\big[1, \frac{2\pi \cdot 5}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 5}{8}\big) = -1.056226$

$a\big[1, \frac{2\pi \cdot 6}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 6}{8}\big) = -1.124652$

$a\big[1, \frac{2\pi \cdot 7}{8}, 0\big] = 2f\big(\frac{2\pi \cdot 7}{8}\big) = -0.932522$

and formula (13.47) reduces to

$b[1, \alpha, 0] = 0$

which gives us

$b\big[1, \frac{2\pi \cdot 0}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 1}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 2}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 3}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 4}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 5}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 6}{8}, 0\big] = 0$

$b\big[1, \frac{2\pi \cdot 7}{8}, 0\big] = 0$

Next we calculate the numbers $a[1, \alpha, 1]$ and $b[1, \alpha, 1]$ using equations (13.50), which tell us that

$a[1, \alpha, 1] = a[1, \alpha, 0] = 2f(\alpha)$

$b[1, \alpha, 1] = -b[1, \alpha, 0] = 0$

Thus, the numbers $a[1, \alpha, 1]$ and $b[1, \alpha, 1]$ are exactly the same as the numbers $a[1, \alpha, 0]$ and $b[1, \alpha, 0]$ in this first iteration. Writing them out explicitly:

$a\big[1, \frac{2\pi \cdot 0}{8}, 1\big] = -0.224356$

$a\big[1, \frac{2\pi \cdot 1}{8}, 1\big] = 2.159318$

$a\big[1, \frac{2\pi \cdot 2}{8}, 1\big] = 4.345334$

$a\big[1, \frac{2\pi \cdot 3}{8}, 1\big] = 0.753214$

$a\big[1, \frac{2\pi \cdot 4}{8}, 1\big] = -0.642824$

$a\big[1, \frac{2\pi \cdot 5}{8}, 1\big] = -1.056226$

$a\big[1, \frac{2\pi \cdot 6}{8}, 1\big] = -1.124652$

$a\big[1, \frac{2\pi \cdot 7}{8}, 1\big] = -0.932522$

$b\big[1, \frac{2\pi \cdot 0}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 1}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 2}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 3}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 4}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 5}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 6}{8}, 1\big] = 0$

$b\big[1, \frac{2\pi \cdot 7}{8}, 1\big] = 0$

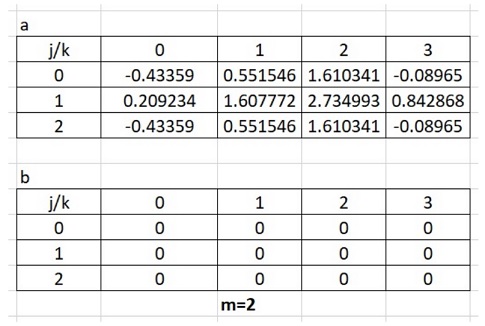
The above results can be summarised in a table for convenience:

We are now ready to begin the second iteration. The iteration variable becomes $m = 2$ and we will have $j = 0, 1$ , $k = 0, 1, 2, 3$ . We compute the numbers $a[2, \alpha, 0]$ , $a[2, \alpha, 1]$ , $b[2, \alpha, 0]$ and $b[2, \alpha, 1]$ using formulas (13.48) and (13.49). We get the formulas

$a[2, \alpha, 0] = \frac{1}{2}\big\{a[1, \alpha, 0] + \cos(\pi \cdot 0/1)a[1, \alpha + \frac{\pi}{1}, 0] - \sin(\pi \cdot 0/1)b[1, \alpha + \frac{\pi}{1}, 0]\big\}$

$= \frac{1}{2}\big\{a[1, \frac{2\pi \cdot k}{8}, 0] + a[1, \frac{2\pi}{8}(k + 4), 0]\big\}$

$a[2, \alpha, 1] = \frac{1}{2}\big\{a[1, \alpha, 1] + \cos(\pi \cdot 1/1)a[1, \alpha + \frac{\pi}{1}, 1] - \sin(\pi \cdot 1/1)b[1, \alpha + \frac{\pi}{1}, 1]\big\}$

$= \frac{1}{2}\big\{a[1, \frac{2\pi \cdot k}{8}, 1] - a[1, \frac{2\pi}{8}(k + 4), 1]\big\}$

$b[2, \alpha, 0] = \frac{1}{2}\big\{b[1, \alpha, 0] + \sin(\pi \cdot 0/1)a[1, \alpha + \frac{\pi}{1}, 0] + \cos(\pi \cdot 0/1)b[1, \alpha + \frac{\pi}{1}, 0]\big\} = 0$

$b[2, \alpha, 1] = \frac{1}{2}\big\{b[1, \alpha, 1] + \sin(\pi \cdot 1/1)a[1, \alpha + \frac{\pi}{1}, 1] + \cos(\pi \cdot 1/1)b[1, \alpha + \frac{\pi}{1}, 1]\big\} = 0$

These then give us the values

$a[2, \frac{2\pi \cdot 0}{8}, 0] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 0}{8}, 0] + a[1, \frac{2\pi}{8}(0+ 4), 0]\big\}$

$= \frac{1}{2}(-0.224356 - 0.642824) = -0.43359$

$a[2, \frac{2\pi \cdot 1}{8}, 0] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 1}{8}, 0] + a[1, \frac{2\pi}{8}(1+ 4), 0]\big\}$

$= \frac{1}{2}(2.159318 - 1.056226) = 0.551546$

$a[2, \frac{2\pi \cdot 2}{8}, 0] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 2}{8}, 0] + a[1, \frac{2\pi}{8}(2+ 4), 0]\big\}$

$= \frac{1}{2}(4.345334 - 1.124652) = 1.610341$

$a[2, \frac{2\pi \cdot 3}{8}, 0] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 3}{8}, 0] + a[1, \frac{2\pi}{8}(3+ 4), 0]\big\}$

$= \frac{1}{2}(0.753214 - 0.932522) = -0.089654$

$a[2, \frac{2\pi \cdot 0}{8}, 1] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 0}{8}, 1] - a[1, \frac{2\pi}{8}(0+ 4), 1]\big\}$

$= \frac{1}{2}(-0.224356 + 0.642824) = 0.209234$

$a[2, \frac{2\pi \cdot 1}{8}, 1] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 1}{8}, 1] - a[1, \frac{2\pi}{8}(1+ 4), 1]\big\}$

$= \frac{1}{2}(2.159318 + 1.056226) = 1.607772$

$a[2, \frac{2\pi \cdot 2}{8}, 1] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 2}{8}, 1] - a[1, \frac{2\pi}{8}(2+ 4), 1]\big\}$

$= \frac{1}{2}(4.345334 + 1.124652) = 2.734993$

$a[2, \frac{2\pi \cdot 3}{8}, 1] = \frac{1}{2}\big\{a[1, \frac{2\pi \cdot 3}{8}, 1] - a[1, \frac{2\pi}{8}(3+ 4), 1]\big\}$

$= \frac{1}{2}(0.753214 + 0.932522) = 0.842868$ $b[2, \frac{2\pi \cdot 0}{8}, 0] = 0$ $b[2, \frac{2\pi \cdot 1}{8}, 0] = 0$

$b[2, \frac{2\pi \cdot 2}{8}, 0] = 0$ $b[2, \frac{2\pi \cdot 3}{8}, 0] = 0$

$b[2, \frac{2\pi \cdot 0}{8}, 1] = 0$ $b[2, \frac{2\pi \cdot 1}{8}, 1] = 0$

$b[2, \frac{2\pi \cdot 2}{8}, 1] = 0$

$b[2, \frac{2\pi \cdot 3}{8}, 1] = 0$

Next we calculate the numbers $a[2, \alpha, 2]$ and $b[2, \alpha, 2]$ using equations (13.50), which tell us that

$a[2, \alpha, 2] = a[2, \alpha, 0]$

$b[2, \alpha, 2] = -b[2, \alpha, 0] = 0$

Thus, the numbers $a[2, \alpha, 2]$ and $b[2, \alpha, 2]$ are exactly the same as the numbers $a[2, \alpha, 0]$ and $b[2, \alpha, 0]$ in the second iteration. Writing them out explicitly:

$a[2, \frac{2\pi \cdot 0}{8}, 2] = -0.43359$

$a[2, \frac{2\pi \cdot 1}{8}, 2] = 0.551546$

$a[2, \frac{2\pi \cdot 2}{8}, 2] = 1.610341$

$a[2, \frac{2\pi \cdot 3}{8}, 2] = -0.089654$

$b[2, \frac{2\pi \cdot 0}{8}, 2] = 0$

$b[2, \frac{2\pi \cdot 1}{8}, 2] = 0$

$b[2, \frac{2\pi \cdot 2}{8}, 2] = 0$

$b[2, \frac{2\pi \cdot 3}{8}, 2] = 0$

The above results are summarised in the following table for convenience:

We are now ready to begin the third iteration. The iteration variable becomes $m = 4$ and we will have $j = 0, 1, 2$ , $k = 0, 1$ . We compute the numbers $a[4, \alpha, 0]$ , $a[4, \alpha, 1]$ , $a[4, \alpha, 2]$ , $b[4, \alpha, 0]$ , $b[4, \alpha, 1]$ and $b[4, \alpha, 2]$ using formulas (13.48) and (13.49). We get the formulas

$a[4, \alpha, 0] = \frac{1}{2}\big\{a[2, \alpha, 0] + \cos(\pi \cdot 0/2)a[2, \alpha + \frac{\pi}{2}, 0] - \sin(\pi \cdot 0/2)b[2, \alpha + \frac{\pi}{2}, 0]\big\}$

$= \frac{1}{2}\big\{a[2, \frac{2\pi \cdot k}{8}, 0] + a[2, \frac{2\pi}{8}(k + 2), 0]\big\}$

$a[4, \alpha, 1] = \frac{1}{2}\big\{a[2, \alpha, 1] + \cos(\pi \cdot 1/2)a[2, \alpha + \frac{\pi}{2}, 1] - \sin(\pi \cdot 1/2)b[2, \alpha + \frac{\pi}{2}, 1]\big\}$

$= \frac{1}{2}a[2, \frac{2\pi \cdot k}{8}, 1]$

$a[4, \alpha, 2] = \frac{1}{2}\big\{a[2, \alpha, 2] + \cos(\pi \cdot 2/2)a[2, \alpha + \frac{\pi}{2}, 2] - \sin(\pi \cdot 2/2)b[2, \alpha + \frac{\pi}{2}, 2]\big\}$

$= \frac{1}{2}\big\{a[2, \frac{2\pi \cdot k}{8}, 2] - a[2, \frac{2\pi}{8}(k + 2), 2]\big\}$

$b[4, \alpha, 0] = \frac{1}{2}\big\{b[2, \alpha, 0] + \sin(\pi \cdot 0/2)a[2, \alpha + \frac{\pi}{2}, 0] + \cos(\pi \cdot 0/2)b[2, \alpha + \frac{\pi}{2}, 0]\big\} = 0$

$b[4, \alpha, 1] = \frac{1}{2}\big\{b[2, \alpha, 1] + \sin(\pi \cdot 1/2)a[2, \alpha + \frac{\pi}{2}, 1] + \cos(\pi \cdot 1/2)b[2, \alpha + \frac{\pi}{2}, 1]\big\}$

$= \frac{1}{2} a[2, \frac{2\pi}{8}(k+2), 1]$

$b[4, \alpha, 2] = \frac{1}{2}\big\{b[2, \alpha, 2] + \sin(\pi \cdot 2/2)a[2, \alpha + \frac{\pi}{2}, 2] + \cos(\pi \cdot 2/2)b[2, \alpha + \frac{\pi}{2}, 2]\big\} = 0$

These then give us the values

$a[4, \frac{2\pi \cdot 0}{8}, 0] = \frac{1}{2}\big\{a[2, \frac{2\pi \cdot 0}{8}, 0] + a[2, \frac{2\pi}{8}(0 + 2), 0]\big\}$

$= \frac{1}{2}(-0.43359 + 1.610341) = 0.5883755$

$a[4, \frac{2\pi \cdot 1}{8}, 0] = \frac{1}{2}\big\{a[2, \frac{2\pi \cdot 1}{8}, 0] + a[2, \frac{2\pi}{8}(1 + 2), 0]\big\}$

$= \frac{1}{2}(0.551546 - 0.089654) = 0.230946$

$a[4, \frac{2\pi \cdot 0}{8}, 1] = \frac{1}{2}a[2, \frac{2\pi \cdot 0}{8}, 1]$

$= \frac{1}{2} \cdot 0.209234 = 0.104617$

$a[4, \frac{2\pi \cdot 1}{8}, 1] = \frac{1}{2}a[2, \frac{2\pi \cdot 1}{8}, 1]$

$= \frac{1}{2} \cdot 1.607772 = 0.803886$

$a[4, \frac{2\pi \cdot 0}{8}, 2] = \frac{1}{2}\big\{a[2, \frac{2\pi \cdot 0}{8}, 2] - a[2, \frac{2\pi}{8}(0 + 2), 2]\big\}$

$= \frac{1}{2}(-0.43359 - 1.610341) = -1.0219655$

$a[4, \frac{2\pi \cdot 1}{8}, 2] = \frac{1}{2}\big\{a[2, \frac{2\pi \cdot 1}{8}, 2] - a[2, \frac{2\pi}{8}(1 + 2), 2]\big\}$

$= \frac{1}{2}(0.551546 + 0.089654) = 0.3206$

$b[4, \frac{2\pi \cdot 0}{8}, 0] = 0$

$b[4, \frac{2\pi \cdot 1}{8}, 0] = 0$

$b[4, \frac{2\pi \cdot 0}{8}, 1] = \frac{1}{2} a[2, \frac{2\pi}{8}(0+2), 1]$

$= \frac{1}{2} \cdot 2.734993 = 1.3674965$

$b[4, \frac{2\pi \cdot 1}{8}, 1] = \frac{1}{2} a[2, \frac{2\pi}{8}(1+2), 1]$

$= \frac{1}{2} \cdot 0.842868 = 0.421434$

$b[4, \frac{2\pi \cdot 0}{8}, 2] = 0$

$b[4, \frac{2\pi \cdot 1}{8}, 2] = 0$

Next we calculate the numbers $a[4, \alpha, 3]$ , $a[4, \alpha, 4]$ , $b[4, \alpha, 3]$ and $b[4, \alpha, 4]$ using equations (13.50), which tell us that

$a[4, \alpha, 3] = a[4, \alpha, 1]$

$a[4, \alpha, 4] = a[4, \alpha, 0]$

$b[4, \alpha, 3] = -b[4, \alpha, 1]$

$b[4, \alpha, 4] = -b[4, \alpha, 0]$

Thus, we can use the previously computed values for $a$ and $b$ in the third iteration to get these. Writing them out explicitly:

$a[4, \frac{2\pi \cdot 0}{8}, 3] = 0.104617$

$a[4, \frac{2\pi \cdot 1}{8}, 3] = 0.803886$

$a[4, \frac{2\pi \cdot 0}{8}, 4] = 0.5883755$

$a[4, \frac{2\pi \cdot 1}{8}, 4] = 0.230946$

$b[4, \frac{2\pi \cdot 0}{8}, 3] = -1.3674965$

$b[4, \frac{2\pi \cdot 1}{8}, 3] = -0.421434$

$b[4, \frac{2\pi \cdot 0}{8}, 4] = 0$

$b[4, \frac{2\pi \cdot 1}{8}, 4] = 0$

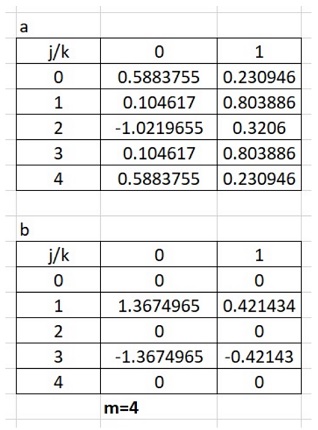
The above results are summarised in the following table:

We are now ready to begin the fourth (and final) iteration. The iteration variable becomes $m = 8$ and we have $j = 0, 1, 2, 3, 4$ , $k = 0$ . We compute the numbers $a[8, 0, 0]$ , $a[8, 0, 1]$ , $a[8, 0, 2]$ , $a[8, 0, 3]$ , $a[8, 0, 4]$ , $b[8, 0, 0]$ , $b[8, 0, 1]$ , $b[8, 0, 2]$ , $b[8, 0, 3]$ and $b[8, 0, 4]$ using formulas (13.48) and (13.49). We get

$a[8, 0, 0] = \frac{1}{2}\big\{a[4, 0, 0] + \cos(\pi \cdot 0/4)a[4, 0 + \frac{\pi}{4}, 0] - \sin(\pi \cdot 0/4)b[4, 0 + \frac{\pi}{4}, 0]\big\}$

$= \frac{1}{2}\big\{a[4, \frac{2\pi \cdot 0}{8}, 0] + a[4, \frac{2\pi}{8}(0 + 1), 0]\big\} = \frac{1}{2}(0.5883755 + 0.230946) = 0.40966075$

$a[8, 0, 1] = \frac{1}{2}\big\{a[4, 0, 1] + \cos(\pi \cdot 1/4)a[4, 0 + \frac{\pi}{4}, 1] - \sin(\pi \cdot 1/4)b[4, 0 + \frac{\pi}{4}, 1]\big\}$

$= \frac{1}{2}\big\{a[4, \frac{2\pi \cdot 0}{8}, 1] + \frac{1}{\sqrt{2}}a[4, \frac{2\pi}{8}(0 + 1), 1] -\frac{1}{\sqrt{2}}b[4, \frac{2\pi}{8}(0 + 1), 1]\big\}$

$= \frac{1}{2}(0.104617 + \frac{1}{\sqrt{2}} \cdot 0.803886 - \frac{1}{\sqrt{2}} \cdot 0.421434) = 0.187525701$

$a[8, 0, 2] = \frac{1}{2}\big\{a[4, 0, 2] + \cos(\pi \cdot 2/4)a[4, 0 + \frac{\pi}{4}, 2] - \sin(\pi \cdot 2/4)b[4, 0 + \frac{\pi}{4}, 2]\big\}$

$= \frac{1}{2}a[4, \frac{2\pi \cdot 0}{8}, 2] = \frac{1}{2} \cdot (-1.0219655) = -0.51098275$

$a[8, 0, 3] = \frac{1}{2}\big\{a[4, 0, 3] + \cos(\pi \cdot 3/4)a[4, 0 + \frac{\pi}{4}, 3] - \sin(\pi \cdot 3/4)b[4, 0 + \frac{\pi}{4}, 3]\big\}$

$= \frac{1}{2}\big\{a[4, \frac{2\pi \cdot 0}{8}, 3] - \frac{1}{\sqrt{2}}a[4, \frac{2\pi}{8}(0 + 1), 3] -\frac{1}{\sqrt{2}}b[4, \frac{2\pi}{8}(0 + 1), 3]\big\}$

$= \frac{1}{2}(0.104617 - \frac{1}{\sqrt{2}} \cdot 0.803886 + \frac{1}{\sqrt{2}} \cdot 0.421434) = -0.082908701$

$a[8, 0, 4] = \frac{1}{2}\big\{a[4, 0, 4] + \cos(\pi \cdot 4/4)a[4, 0 + \frac{\pi}{4}, 4] - \sin(\pi \cdot 4/4)b[4, 0 + \frac{\pi}{4}, 4]\big\}$

$= \frac{1}{2}(a[4, \frac{2\pi \cdot 0}{8}, 4] - a[4, \frac{2\pi}{8}(0 + 1), 4]) = \frac{1}{2} (0.5883755 - 0.230946) = 0.17871475$

$b[8, 0, 0] = \frac{1}{2}\big\{b[4, 0, 0] + \sin(\pi \cdot 0/4)a[4, 0 + \frac{\pi}{4}, 0] + \cos(\pi \cdot 0/4)b[4, \frac{2\pi}{8}(0 + 1), 0]\big\}$

$= 0$ $b[8, 0, 1] = \frac{1}{2}\big\{b[4, 0, 1] + \sin(\pi \cdot 1/4)a[4, 0 + \frac{\pi}{4}, 1] + \cos(\pi \cdot 1/4)b[4, 0 + \frac{\pi}{4}, 1]\big\}$

$= \frac{1}{2}(b[4, 0, 1] + \frac{1}{\sqrt{2}} \cdot a[4, \frac{2\pi}{8}(0 + 1), 1] + \frac{1}{\sqrt{2}} \cdot b[4, \frac{2\pi}{8}(0 + 1), 1])$

$= \frac{1}{2}(1.3674965 + \frac{1}{\sqrt{2}} \cdot 0.803886 + \frac{1}{\sqrt{2}} \cdot 0.421434) = 1.116964291$

$b[8, 0, 2] = \frac{1}{2}\big\{b[4, 0, 2] + \sin(\pi \cdot 2/4)a[4, 0 + \frac{\pi}{4}, 2] + \cos(\pi \cdot 2/4)b[4, 0 + \frac{\pi}{4}, 2]\big\}$

$= \frac{1}{2} \cdot a[4, \frac{2\pi}{8}(0 + 1), 2] = \frac{1}{2} \cdot 0.3206 = 0.1603$

$b[8, 0, 3] = \frac{1}{2}\big\{b[4, 0, 3] + \sin(\pi \cdot 3/4)a[4, 0 + \frac{\pi}{4}, 3] + \cos(\pi \cdot 3/4)b[4, 0 + \frac{\pi}{4}, 3]\big\}$

$= \frac{1}{2}(b[4, 0, 3] + \frac{1}{\sqrt{2}} \cdot a[4, \frac{2\pi}{8}(0 + 1), 3] - \frac{1}{\sqrt{2}} \cdot b[4, \frac{2\pi}{8}(0 + 1), 3])$

$= \frac{1}{2}(-1.3674965 + \frac{1}{\sqrt{2}} \cdot 0.803886 + \frac{1}{\sqrt{2}} \cdot 0.421434) = -0.250532209$

$b[8, 0, 4] = \frac{1}{2}\big\{b[4, 0, 4] + \sin(\pi \cdot 4/4)a[4, 0 + \frac{\pi}{4}, 4] + \cos(\pi \cdot 4/4)b[4, 0 + \frac{\pi}{4}, 4]\big\} = 0$

The above results are summarised in the following table:

The required approximation is then

$q(x) = 0.204830375+0.187525701\cos(x)+1.116964291\sin(x)$

$-0.51098275\cos(2x)+0.1603\sin(2x)$

$-0.082908701\cos(3x)-0.250532209\sin(3x)$

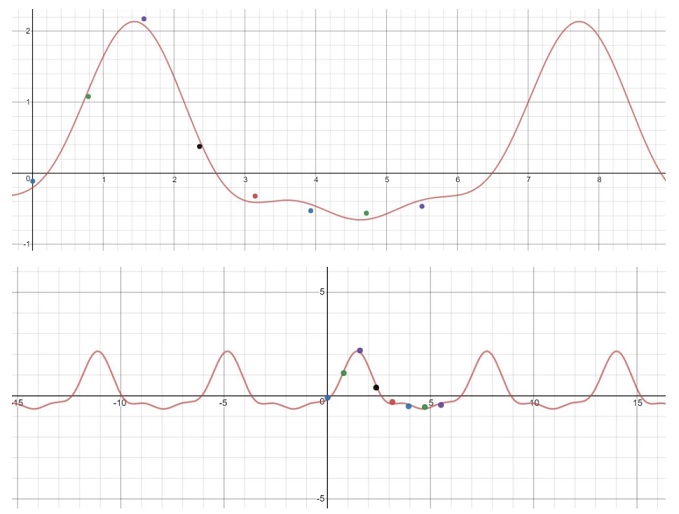
The graph of $q(x)$ is plotted in the figures below for comparison with the initial data (the second figure shows more of the periodic pattern):

Fast Fourier Transform by hand

Published by Dr Christian P. H. Salas

Leave a comment Cancel reply