Zero-field singularity of magnetic susceptibility in a 4-D Ising model

For the purposes of a lecture on simulating the Ising model of ferromagnetism using the Metropolis-Hastings algorithm, I explored the behaviour of magnetic susceptibility on a four-dimensional hypercube lattice. In particular, I wanted to test a well-known prediction of theoretical physics that a zero-field singularity should appear at a certain critical temperature. The idea is that there is an essential singularity in the mathematics at zero external magnetic field which disappears with a non-zero magnetic field. See the discussion on physics Stack Exchange about this. I was interested to see if a computer simulation of magnetic susceptibility in an Ising model on a four-dimensional hypercube lattice would produce similar results as the second diagram in this Stack Exchange query, which I reproduce here:

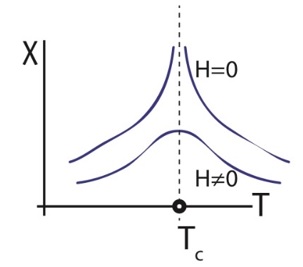
The results do suggest that, in the nearest-neighbour ferromagnetic Ising model on a 4-D hypercube lattice, there is a cusp-like singularity in magnetic susceptibility at a critical temperature around T = 7. This singularity becomes more and more apparent in the plots as the external magnetic field strength is reduced to zero but tends to disappear as the field strength increases. I want to record this experiment and the results in the present post.

I considered a 4-D ferromagnetic Ising model on a hypercubic lattice, $\mathcal{L}={a \mathbf{i}+ b \mathbf{j} + c \mathbf{k} + d \mathbf{l}}$ with $a, b, c, d = 1, 2, \ldots, L$ . I assumed periodic boundary conditions and the presence of an external magnetic field with parameter $B$ . The nearest-neighbour Hamiltonian for a particular configuration $\mathbf{s}$ of the $N = L^4$ spins on the four-dimensional hypercube is

$E(\mathbf{s}, J, B) = -J \sum_{\mathbf{d} \in \mathcal{L}} s_{\mathbf{d}}(s_{\mathbf{d}+ \mathbf{i}}+s_{\mathbf{d}+ \mathbf{j}} + s_{\mathbf{d}+ \mathbf{k}}+s_{\mathbf{d}+ \mathbf{l}}) - B \sum_{\mathbf{d} \in \mathcal{L}} s_{\mathbf{d}} \quad \quad \quad \quad (1)$

where $s_{\mathbf{d}}$ is the spin at site $\mathbf{d}$ on the lattice, $J > 0$ is the nearest-neighbour interaction energy and $B > 0$ is the external magnetic field parameter. The partition function assuming thermal equilibrium at a temperature $T$ is

$Z = \sum_{i=1}^{2^N} \exp \big(-\frac{E_i}{k_B T}\big) \quad \quad \quad \quad (2)$

where $k_B$ is Boltzmann’s constant and $E_i$ is the Hamiltonian for the $i$ -th spin configuration $\mathbf{s}_i$ . For the computer simulations I used units in which $J = 1$ and $k_B = 1$ .

I used Monte Carlo simulations in the form of the well-known single-flip Metropolis-Hastings algorithm to produce plots of the magnetic susceptibility, $\chi$ , as a function of the temperature in the range $T = 0.5$ to $T = 15.0$ , for a lattice of size $N = L \times L \times L \times L$ with $L = 5$ , $L = 10$ and $L = 15$ . With units in which $J = 1$ and $k_B = 1$ , the magnetic susceptibility is calculated as

$\chi =\frac{1}{T N}\big(\langle S^2 \rangle - \langle S \rangle^2\big) \quad \quad \quad \quad (3)$

where

$S=\sum_{\mathbf{d} \in \mathcal{L}} s_{\mathbf{d}} \quad \quad \quad \quad (4)$

is the total magnetisation given a particular spin configuration $\mathbf{s}$ on the 4-D lattice.

I initially chose a range of $B$ -values rising from $0.05$ to $0.8$ in multiples of two. I obtained the following results for $L = 5$ , $L = 10$ and $L = 15$ , starting with a completely ordered configuration in which all the spins in the lattice were in the $+1$ state:

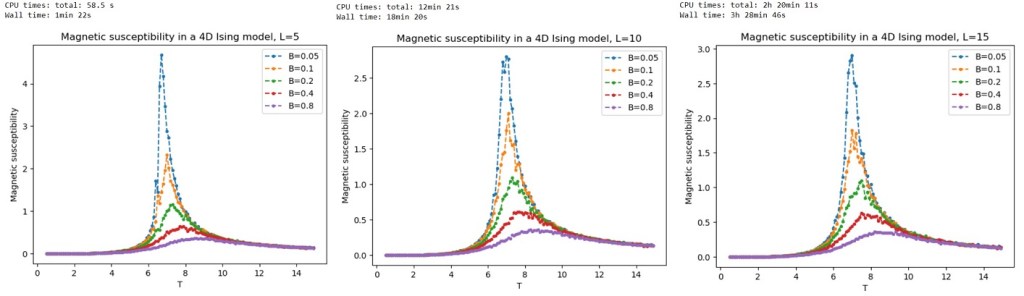
The results show a clear peak in magnetic susceptibility becoming more pronounced as $B$ is reduced towards zero, with the critical temperature being around $T = 7$ . Notice also a rapid increase in the CPU time with $L$ , the CPU time being around one minute for $L = 5$ , twelve minutes for $L = 10$ , and over two hours for $L = 15$ . The plot did not change much between $L = 10$ and $L = 15$ so I used $L = 10$ for the remaining simulations.

To confirm the zero-field singularity at the critical temperature $T = 7$ , I reduced $B$ even further. I obtained the following plots for $B$ -values going down to $B = 0.0001953125$ .

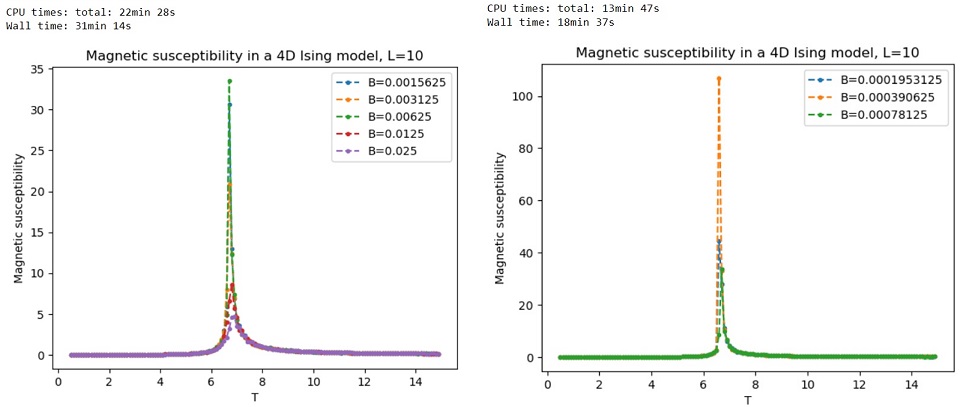
It is clear that the peak becomes arbitrarily large as $B \rightarrow 0$ at a critical temperature of around $T = 7$ , indicating that there is indeed a singularity there.

Zero-field singularity of magnetic susceptibility in a 4-D Ising model

Published by Dr Christian P. H. Salas

Leave a comment Cancel reply