Using Prüfer sequences to count and classify irreducible labelled 10-node trees

In the cult classic movie Good Will Hunting (Miramax, 1997), a maths-genius janitor played by a young Matt Damon secretly solves challenge problems in graph theory written on a blackboard by an MIT maths professor for his students.

One of these problems, which Will can be seen solving in the above screenshot from the movie, is the following:

Draw all the homeomorphically irreducible trees with n=10.

Homeomorphically irreducible trees are those which do not contain any vertices of degree 2 and which are non-isomorphic. There are ten such 10-node trees, as follows:

There are many articles and videos online which discuss how these ten trees can be deduced in various ways. However, two questions which have always bothered me since I first saw the movie do not seem to have been discussed anywhere. While preparing an introductory lecture on trees in graph theory, I decided to try to answer these questions once and for all and am recording the results in the present post. (I also presented these results in my lecture!)

By Cayley’s famous formula $n^{n-2}$ for the number of labelled trees with $n$ vertices, there are 100 million labelled 10-node trees. I always wondered how many of these 100 million labelled 10-node trees are irreducible, and how many of the irreducible labelled trees belong to each of the ten homeomorphically irreducible types in the Good Will Hunting problem? Below, I first use combinatorial arguments to calculate the number of irreducible labelled 10-node trees and then confirm this figure using Python. I also use Python to classify the irreducible labelled trees into the ten Good Will Hunting isomorphism classes.

Combinatorial calculations

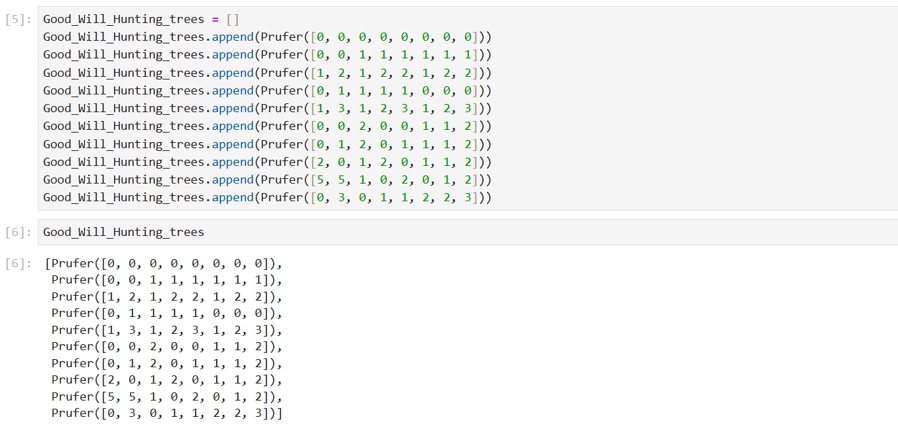
To calculate the total number of irreducible labelled 10-node trees, we begin by observing that the Prüfer sequences of these trees will all be 8 digits long and such that no number occurs with a frequency of 1 (the degree of a vertex in a tree is one more than the frequency of occurrence of the vertex label in the tree’s Prüfer sequence, so the Prüfer sequences of trees which do not contain vertices of degree 2 cannot contain vertex labels with a frequency of 1). To illustrate this, I randomly assigned labels to the ten non-isomorphic trees from the Good Will Hunting problem above and calculated their Prüfer sequences as follows:

As expected, all the vertex labels in the Prüfer sequences above appear with frequencies of at least 2. Therefore, the combinatorial problem we need to solve is the following:

How many ways are there to form a sequence of 8 numbers chosen from the ten numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, in such a way that each number that appears in the sequence appears at least twice?

We will need to use a standard result from combinatorics which says that if there are $n$ objects, with $r_1$ of type 1, $r_2$ of type 2, . . . , and $r_m$ of type $m$ , where $r_1 + r_2 + \cdots + r_m = n$ , then the number of arrangements of these objects, denoted $P(n; r_1, r_2, \ldots, r_m)$ , is

$P(n; r_1, r_2, \ldots, r_m) = \frac{n!}{r_1! r_2! \cdots r_m!} \qquad \qquad \qquad \qquad \qquad (1)$

To apply this result, we need to identify all the possible patterns of 8-digit arrangements satisfying the above conditions, then apply the formula to each possible pattern to find out how many ways there are to arrange the 8 digits in that pattern. Adding up all the possible ways of arranging the 8 digits in each pattern will then give the total number of irreducible labelled 10-node trees. There are actually only seven cases that need to be considered. Using letters to stand for numbers, only the following seven patterns are possible:

Case 1: $(a, a, a, a, a, a, a, a)$

Here, only a single number appears in the Prüfer sequence. There are 10 options for choosing which number occurs 8 times in this sequence, so there are 10 ways to arrange a Prüfer sequence in which one number occurs 8 times.

Case 2: $(a, a, a, a, a, a, b, b)$

Here, only two numbers appear in the Prüfer sequence, one of them 6 times and the other 2 times. There are 10 options for choosing which number occurs 6 times and then 9 options for choosing which number occurs 2 times. Using formula (1) above, there are $P(8; 6, 2) = \frac{8!}{6!2!} = 28$ ways to arrange 6 of one number and 2 of the other. Thus, there are $\frac{10 \times 9 \times 8!}{6!2!} = \frac{10!}{6!2!} = 2520$ ways to arrange a Prüfer sequence in which one number occurs 6 times and another occurs twice.

Case 3: $(a, a, a, a, a, b, b, b)$

Here, only two numbers appear in the Prüfer sequence, one of them 5 times and the other 3 times. There are 10 options for choosing which number occurs 5 times and then 9 options for choosing which number occurs 3 times. Using formula (1) above, there are $P(8; 5, 3) = \frac{8!}{5!3!} = 56$ ways to arrange 5 of one number and 3 of the other. Thus, there are $\frac{10 \times 9 \times 8!}{5!3!} = \frac{10!}{5!3!} = 5040$ ways to arrange a Prüfer sequence in which one number occurs 5 times and another occurs 3 times.

Case 4: $(a, a, a, a, b, b, b, b)$

Here, only two numbers appear in the Prüfer sequence, each of them 4 times. There are 10 options for choosing a first number which occurs 4 times and then 9 options for choosing a second number which occurs 4 times. When considering the possible arrangements, we note that the numbers can be interchanged without affecting each given arrangement because they occur with the same frequency, so there are two equivalent versions of each arrangement. Thus, using formula (1) above, there are $\frac{1}{2} P(8; 4, 4) = \frac{1}{2}\frac{8!}{4!4!} = 35$ ways to arrange 4 of one number and 4 of the other. Thus, there are $\frac{10 \times 9 \times 8!}{2 \times 4!4!} = \frac{10!}{2 \times 4!4!} = 3150$ ways to arrange a Prüfer sequence in which one number occurs 4 times and another occurs 4 times.

Case 5: $(a, a, b, b, c, c, c, c)$

Here, three different numbers appear in the Prüfer sequence, one of them 4 times and the other two twice. There are 10 options for choosing a first number which occurs 4 times, then 9 options for choosing a second number which occurs 2 times, then 8 options for choosing a third number which occurs 2 times. When considering the possible arrangements, we note that the two numbers which occur twice can be interchanged without affecting each given arrangement because they occur with the same frequency, so there are two equivalent versions of each arrangement. Thus, using formula (1) above, there are $\frac{1}{2} P(8; 4, 2, 2) = \frac{1}{2}\frac{8!}{2!2!4!} = 35$ ways to arrange 4 of one number and 2 of each of the other two numbers. Thus, there are $\frac{10 \times 9 \times 8 \times 8!}{2 \times 2!2!4!} = 4 \times \frac{10!}{2!2!4!} = 151200$ ways to arrange a Prüfer sequence in which one number occurs 4 times and two other numbers occur 2 times each.

Case 6: $(a, a, a, b, b, b, c, c)$

Here, three different numbers appear in the Prüfer sequence, one of them 2 times and the other two 3 times. There are 10 options for choosing a first number which occurs 2 times, then 9 options for choosing a second number which occurs 3 times, then 8 options for choosing a third number which occurs 3 times. When considering the possible arrangements, we note that the two numbers which occur 3 times can be interchanged without affecting each given arrangement because they occur with the same frequency, so there are two equivalent versions of each arrangement. Thus, using formula (1) above, there are $\frac{1}{2} P(8; 2, 3, 3) = \frac{1}{2}\frac{8!}{2!3!3!} = 280$ ways to arrange 2 of one number and 3 of each of the other two numbers. Thus, there are $\frac{10 \times 9 \times 8 \times 8!}{2 \times 2!3!3!} = 4 \times \frac{10!}{2!3!3!} = 201600$ ways to arrange a Prüfer sequence in which one number occurs 2 times and two other numbers occur 3 times each.

Case 7: $(a, a, b, b, c, c, d, d)$

Finally, four different numbers appear in this case, each of them 2 times. There are 10 options for choosing a first number which occurs 2 times, then 9 options for choosing a second, then 8 options for choosing a third, then 7 options for choosing the fourth. When considering the possible arrangements, we note that the four numbers which occur 2 times can be interchanged without affecting each given arrangement because they occur with the same frequency, so there are $4 \times 3 \times 2 \times 1 = 24$ equivalent versions of each arrangement. Thus, using formula (1) above, there are $\frac{1}{24} P(8; 2, 2, 2, 2) = \frac{1}{24}\frac{8!}{2!2!2!2!} = 105$ ways to arrange 2 each of four numbers. Thus, there are $\frac{10 \times 9 \times 8 \times 7 \times 8!}{24 \times 2!2!2!2!} = \frac{7}{3} \times \frac{10!}{2!2!2!2!} = 529200$ ways to arrange a Prüfer sequence in which four different numbers occur 2 times each.

Adding up the totals for the seven cases above, we find

$10 + 2520 + 5040 + 3150 + 151200 + 201600 + 529200 = 892720$

Thus, according to the combinatorial calculation approach above, there are 892720 irreducible labelled 10-node trees. This will now be confirmed computationally using Python, and the 892720 trees will also be classified into the ten Good Will Hunting isomorphism types.

Python calculations

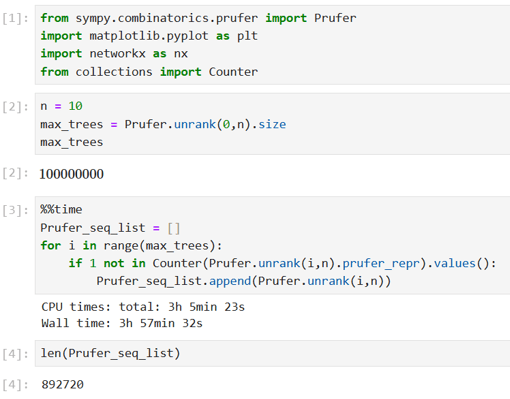
To confirm the number of irreducible labelled 10-node trees, I wrote the following Python code to pick from the 100 million labelled 10-node trees those whose Prüfer sequences do not contain vertex labels with a frequency of 1. As can be seen from the output, this took nearly 4 hours (on a laptop with 16.0GB of RAM) and confirmed the number 892720 obtained via the combinatorial calculations above.

I then wrote the following Python code to classify the 892720 irreducible trees into the ten Good Will Hunting isomorphism types. This code uses the Prüfer sequences I calculated for the randomly labelled ten isomorphism types above as templates against which each of the 892720 trees can be checked. Each tree is then classified into one of the ten types depending on which of the ten Prüfer sequences it is isomorphic to.

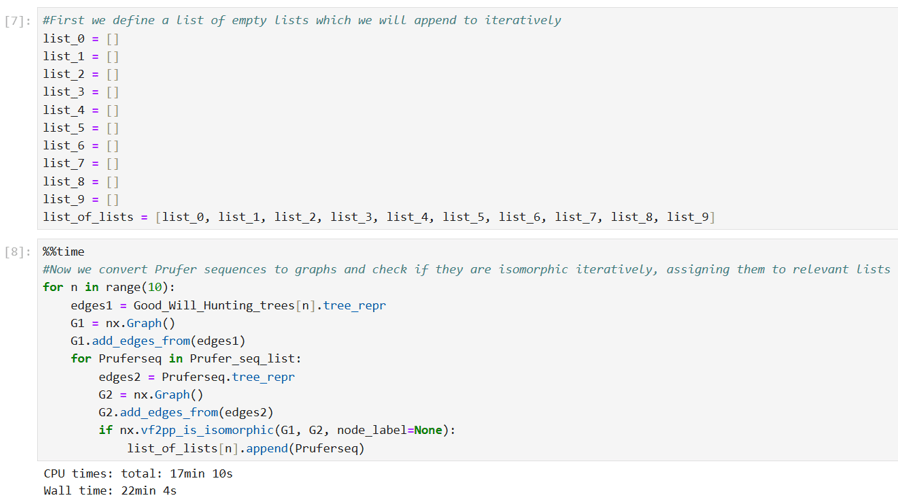
As can be seen from the output here, this classification process took 22 minutes. The results showing the classification of the 892720 trees into the ten Good Will Hunting isomorphism types are shown below, together with a check that the ten totals do indeed account for all the 892720 irreducible trees.

Using Prüfer sequences to count and classify irreducible labelled 10-node trees

Published by Dr Christian P. H. Salas

Leave a comment Cancel reply