Quantum mechanical models in three dimensions and involving many particles, etc., use a formalism which is largely based on some key mathematical modelling ideas pertaining to single particle systems. These mathematical modelling ideas are principally designed to tell us what sets of values we are `allowed’ to observe when we measure some aspect of a quantum system, and with what probabilities we can expect to observe particular values from these sets. For quick reference, I wanted to have a relatively brief and coherent overview of these key mathematical ideas and have written the present note for this purpose. Dirac notation is used throughout.
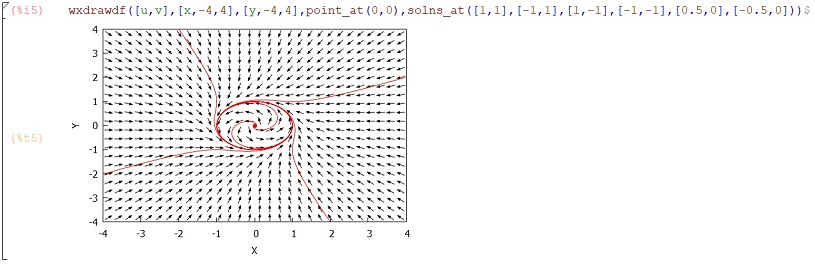
Quantum particle in a ring
To start with, suppose all we know is that a quantum particle in a closed ring of length 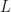 has a given linear momentum
has a given linear momentum  when an observation of its position is made. The result of the observation is that the particle will be found at some point
when an observation of its position is made. The result of the observation is that the particle will be found at some point  lying in a small interval of length
lying in a small interval of length 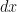 on the closed ring. We assume that the radius of the ring is sufficiently large to make angular momentum considerations negligible. De Broglie tells us that the linear momentum of the quantum particle must be associated with a wavelength
on the closed ring. We assume that the radius of the ring is sufficiently large to make angular momentum considerations negligible. De Broglie tells us that the linear momentum of the quantum particle must be associated with a wavelength  of some wave function
of some wave function  according to the rule
according to the rule

where 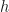 is Planck’s constant. (There is also a fundamental equation
is Planck’s constant. (There is also a fundamental equation  linking the energy of a quantum particle to the frequency of a wave function. This will be introduced later in connection with modelling time evolution in quantum mechanics). Somewhat surprisingly at first sight, this is all the information we need to deduce a precise functional form for the wave function
linking the energy of a quantum particle to the frequency of a wave function. This will be introduced later in connection with modelling time evolution in quantum mechanics). Somewhat surprisingly at first sight, this is all the information we need to deduce a precise functional form for the wave function  as well as the allowed spectrum of momenta for the particle. (Note that
as well as the allowed spectrum of momenta for the particle. (Note that  gives the probability that a particle with momentum
gives the probability that a particle with momentum  will be found at a position
will be found at a position  lying in a small interval of length
lying in a small interval of length 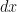 on the closed ring. This probability distribution can be observed through experiment, while
on the closed ring. This probability distribution can be observed through experiment, while  itself is unobservable directly. We refer to
itself is unobservable directly. We refer to  as a quantum mechanical probability amplitude in this connection).
as a quantum mechanical probability amplitude in this connection).
First, we imagine what the position wave function  must look like as a Fourier series. Since only a single wavelength is involved in this particular setup,
must look like as a Fourier series. Since only a single wavelength is involved in this particular setup,  must be a pure wave, i.e., the exponential form of its Fourier series must consist of a single term, so we must have
must be a pure wave, i.e., the exponential form of its Fourier series must consist of a single term, so we must have

for some  that still remains to be calculated, where
that still remains to be calculated, where 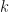 is the wave number
is the wave number

Combining (1) and (3), we can write de Broglie’s linear momentum formula as

where  is the reduced Planck’s constant. We can then rewrite the above wave function to explicitly incorporate momentum as
is the reduced Planck’s constant. We can then rewrite the above wave function to explicitly incorporate momentum as

An assumption called the certainty condition in quantum mechanics, or sometimes the square integrability condition or normalizability condition, is that the quantum particle must be found upon measurement to be located somewhere on the ring, so we must have

(This requires quantum mechanics to take place in a Hilbert space of square-integrable functions, as discussed further below). Substituting our wave function so far into this then gives  , so we can write the full position wave function as
, so we can write the full position wave function as

Second, to deduce the permitted spectrum of momenta, we use the fact that the position wave function for a quantum particle in a ring must be periodic with period 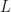 , so we must have
, so we must have

Therefore

which implies

for  , and therefore the permitted spectrum of momenta for this setup is given by
, and therefore the permitted spectrum of momenta for this setup is given by

It is impossible for this quantum particle to have a momentum  that does not belong to this particular discrete spectrum.
that does not belong to this particular discrete spectrum.
In our one-dimensional quantum particle in a ring system, a measurement result that is nondegenerate uniquely defines a state of the system, denoted by a ket  in Dirac notation, e.g.,
in Dirac notation, e.g.,  for a momentum measurement or
for a momentum measurement or  for a position measurement. Formally, as outlined below, these kets are vectors in a Hilbert space. In contrast, a degenerate measurement is a measurement that cannot uniquely define a state of the system, i.e., it is consistent with more than a single state and is thus regarded as a superposition of states. As an example, the energy
for a position measurement. Formally, as outlined below, these kets are vectors in a Hilbert space. In contrast, a degenerate measurement is a measurement that cannot uniquely define a state of the system, i.e., it is consistent with more than a single state and is thus regarded as a superposition of states. As an example, the energy 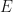 of our particle in a ring system is degenerate because it is a quadratic function of momentum,
of our particle in a ring system is degenerate because it is a quadratic function of momentum,  , and there is nothing in the model to prevent the momentum being negative. Thus, the same value of
, and there is nothing in the model to prevent the momentum being negative. Thus, the same value of 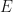 can correspond to a momentum state
can correspond to a momentum state  or a momentum state
or a momentum state  , so the label
, so the label 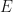 cannot by itself be used to uniquely define a state
cannot by itself be used to uniquely define a state  here.
here.
An event is a measurement finding for a system when it is in a known, i.e., pre-prepared, state. For example, we can measure the position  for our system when we know the quantum particle in the ring has been prepared to have momentum state
for our system when we know the quantum particle in the ring has been prepared to have momentum state  . In quantum mechanics, all such events have probability amplitudes with the property that their absolute value squared gives a probability density for the event, as mentioned above. In this case, as mentioned earlier, the probability amplitude for the position measurement is
. In quantum mechanics, all such events have probability amplitudes with the property that their absolute value squared gives a probability density for the event, as mentioned above. In this case, as mentioned earlier, the probability amplitude for the position measurement is  in Dirac notation, with
in Dirac notation, with  . Note that there is an implicit assumption that the measurement of position occurs instantaneously after the quantum system has been prepared in its initial momentum state, i.e., there should not have been enough time for the system to evolve away from its pre-prepared momentum state before position is measured. This implicit assumption applies to all quantum events. Also note that the famous Dirac delta function in the continuous case (and the Kronecker delta function in the discrete case) arise by considering self-space events, i.e., performing the same measurement twice in rapid succession. For example, suppose the quantum particle is known to be in position state
. Note that there is an implicit assumption that the measurement of position occurs instantaneously after the quantum system has been prepared in its initial momentum state, i.e., there should not have been enough time for the system to evolve away from its pre-prepared momentum state before position is measured. This implicit assumption applies to all quantum events. Also note that the famous Dirac delta function in the continuous case (and the Kronecker delta function in the discrete case) arise by considering self-space events, i.e., performing the same measurement twice in rapid succession. For example, suppose the quantum particle is known to be in position state  and then a second measurement of position is quickly made. The measurement space in this case is continuous and the self-space probability amplitude
and then a second measurement of position is quickly made. The measurement space in this case is continuous and the self-space probability amplitude  is given by the Dirac delta function
is given by the Dirac delta function

which is such that  for
for  , while
, while  for
for  in such a way that
in such a way that  , and which famously also has as its defining property the integral equation
, and which famously also has as its defining property the integral equation

In the case of repeated measurements of momentum, which has a discrete measurement space for the quantum particle in a ring model, the corresponding self-space probability amplitude would be given by the Kronecker delta

which is such that  if
if  , and
, and  if
if  . The Dirac delta function can be thought of as the continuous measurement space analogue of the Kronecker delta for discrete spaces.
. The Dirac delta function can be thought of as the continuous measurement space analogue of the Kronecker delta for discrete spaces.
The abstract measurement space consisting of the spectrum of all possible results you can get from a measurement is a Hilbert space, i.e., a complex inner product space which is also a complete metric space with regard to the distance function induced by the inner product. The state of a physical system is treated as a vector in such a Hilbert space. There is a Hilbert space containing all the possible position and momentum states above, for example, and the probability amplitudes  are formally the inner products of the two state vectors
are formally the inner products of the two state vectors  and
and  in this Hilbert space. A necessary and sufficient condition for these inner products to exist is that the functions involved are square-integrable. The completeness of these measurement spaces means that each can act as a basis, i.e., a ‘language’, in terms of which other states can be represented. Thus, we can regard the probability amplitude
in this Hilbert space. A necessary and sufficient condition for these inner products to exist is that the functions involved are square-integrable. The completeness of these measurement spaces means that each can act as a basis, i.e., a ‘language’, in terms of which other states can be represented. Thus, we can regard the probability amplitude  as the projection of state
as the projection of state  on
on  -space, or the momentum state
-space, or the momentum state  expressed in the language of
expressed in the language of  , or simply the state
, or simply the state  expressed as a function of
expressed as a function of  . Similarly,
. Similarly,  can be interpreted as the position state
can be interpreted as the position state  expressed in the language of
expressed in the language of  . A key axiom of quantum mechanics is that
. A key axiom of quantum mechanics is that  and
and  are related via complex conjugation:
are related via complex conjugation:

So, for example, given  as defined in (7) above, we can immediately deduce that
as defined in (7) above, we can immediately deduce that

(But remember that these probability amplitudes are never directly observable. Only the associated probability distributions are observable experimentally).
We can use this idea of measurement spaces acting as language spaces (or, more formally, basis sets) to express one state as a superposition of other states. For example, a hypothetical state  can be experimentally resolved into momentum state components, expressed mathematically as the superposition
can be experimentally resolved into momentum state components, expressed mathematically as the superposition

This is a discrete sum because recall that, for the quantum particle in a ring model, the measurement space for momentum is discrete. On the right-hand side, each  is a pure momentum state, and the bra-ket
is a pure momentum state, and the bra-ket  is the weight attached to this pure momentum state in the superposition. The same state
is the weight attached to this pure momentum state in the superposition. The same state  can equally well be perceived as a superposition of position states:
can equally well be perceived as a superposition of position states:

The summation here is to be implemented as an integral since the measurement space for position is continuous for the quantum particle in a ring model. Thus, we can write (14) in integral form as

Notice how the delta function definition of the self-space amplitude,  , now arises in this integral when computing the coefficients of the expansion of
, now arises in this integral when computing the coefficients of the expansion of 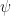 in terms of the continuous position basis:
in terms of the continuous position basis:

Thus, the position space wave functions  , evaluated at particular values of
, evaluated at particular values of  , are just the coefficients of a state
, are just the coefficients of a state  (belonging to Hilbert space) in a superposition using a continuous position basis.
(belonging to Hilbert space) in a superposition using a continuous position basis.
It is useful to bear in mind that these superposition equations are analogous to how a periodic function  can be expanded in a Fourier series. We are using the same kinds of mathematical structures and arguments in defining the superpositions above.
can be expanded in a Fourier series. We are using the same kinds of mathematical structures and arguments in defining the superpositions above.
Both of the superposition equations above are special cases of a general rule called the completeness theorem or superposition theorem, which can be expressed mathematically in Dirac notation as

The ket  on the left-hand side of this equation is a pure
on the left-hand side of this equation is a pure  -state. The bra
-state. The bra  can be regarded here as an operator that, when it is applied to any state
can be regarded here as an operator that, when it is applied to any state  , gives the weight attached to that pure
, gives the weight attached to that pure  -state in the superposition for
-state in the superposition for  :
:

In this last equation, it is as if we are multiplying  on the right-hand side by 1 to get
on the right-hand side by 1 to get  again on the left-hand side, so we represent this situation as in equation (15) above.
again on the left-hand side, so we represent this situation as in equation (15) above.
Measuring an observable for our quantum system, assuming the system has been prepared so that it is in a known state when the measurement takes place, is modelled mathematically as applying a suitable operator to the prepared state ket. If an operator  operates on a state ket
operates on a state ket  , another new state ket is produced denoted by
, another new state ket is produced denoted by  . For each such operator
. For each such operator  , there must be a rule or instruction which tells us what is produced when the ket undergoes the operation. This rule must itself be given in some language, e.g., the representation of
, there must be a rule or instruction which tells us what is produced when the ket undergoes the operation. This rule must itself be given in some language, e.g., the representation of  in
in  -space is denoted
-space is denoted  , and in
, and in  -space is denoted
-space is denoted  . An important example is the operator
. An important example is the operator  whose rule in
whose rule in  -space is take the derivative with respect to x. Therefore, in Dirac notation:
-space is take the derivative with respect to x. Therefore, in Dirac notation:

This equation can be applied to any ket, so for example

In the same way that a state has an existence which is independent of the language used to represent it, so too may operators be expressed in different languages. For example, we can convert an instruction  in
in  -language to an instruction
-language to an instruction  in
in  -language by using a ket-bra sum
-language by using a ket-bra sum  . We get
. We get

No specific state  is involved here, so we can write the general language-translation-rule as
is involved here, so we can write the general language-translation-rule as

To give an example of implementing this in practice, recall that for our quantum particle in a ring system we have

Therefore, the conversion represented by (19) can be written in conventional notation as

Integrating the right-hand side by parts, we find it equals



Therefore,

Since 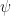 is arbitrary, the general rule is
is arbitrary, the general rule is

The operators that represent measurement of observables in quantum mechanics are linear and hermitian. (A hermitian matrix is the complex analogue of a symmetric matrix. It is equal to its own conjugate transpose. Another type of matrix which arises frequently in quantum mechanics is a unitary matrix. This is the complex analogue of an orthogonal matrix, the latter having the property that the transpose matrix is the inverse. In the case of a unitary matrix, the complex conjugate transpose is the inverse. Hermitian operators are usually related to the measurement of observables in quantum mechanics, whereas unitary operators are related to carrying out processes such as translations of quantum states in space and time. We need to extend the symmetric and orthogonal properties of ordinary matrices to include complex conjugation in the definition of hermitian and unitary matrices to cater for the fact that quantum mechanics involves complex numbers, e.g., in the unitary matrix case, simply transposing a complex matrix and multiplying by the original matrix would in general produce another complex matrix rather than an identity matrix, without the complex conjugation step). As per Sturm-Liouville theory, hermitian operators have the property that their eigenvalues are real and form complete measurement spaces, i.e., they represent the entire spectrum of values that can be observed when a measurement is made. It is important to understand, however, that these eigenvalues are only revealed when the operator is applied to its particular home measurement space, formally called its eigenspace. Each operator is defined in terms of a particular instruction (telling us what the operator does) and in terms of the set of eigenvalues it gives rise to when it is applied to its particular eigenspace. The effect of applying an operator to a ket in its eigenspace will be to produce the same ket multiplied by an eigenvalue of the operator. The kets for which this happens are the eigenkets of the operator. For example, based on the result in (22) above, define a new operator 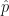 as
as

Then on the basis of (22), we immediately deduce that

This is the bra form of the eigenvalue equation for 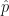 , meaning that in
, meaning that in  -language, which is the language of the eigenspace of
-language, which is the language of the eigenspace of 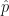 , the effect of
, the effect of 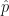 is to multiply any state it operates on by a number
is to multiply any state it operates on by a number  . We can equivalently state the eigenvalue equation in ket form:
. We can equivalently state the eigenvalue equation in ket form:

This is saying that the effect of 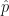 on its eigenket is to produce a number times the same eigenket, no matter what language the instruction for
on its eigenket is to produce a number times the same eigenket, no matter what language the instruction for 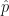 is expressed in. The two forms (24) and (25) are equivalent, and both mean that the operator
is expressed in. The two forms (24) and (25) are equivalent, and both mean that the operator 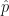 produces the spectrum of momenta for the quantum particle in a ring model, and the eigenkets of
produces the spectrum of momenta for the quantum particle in a ring model, and the eigenkets of 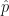 are
are  . We say that the
. We say that the  -space kets
-space kets  are eigenstates of
are eigenstates of 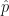 with eigenvalues
with eigenvalues  . Notice that when the operator
. Notice that when the operator  is expressed in
is expressed in  -language instead of
-language instead of  -language, we do not get a proper eigenvalue equation (see (18) above). Therefore,
-language, we do not get a proper eigenvalue equation (see (18) above). Therefore,  -space is not the eigenspace of
-space is not the eigenspace of  . However, when the operator
. However, when the operator  is expressed in
is expressed in  -language, we do get a proper eigenvalue equation (equation (22) above), so
-language, we do get a proper eigenvalue equation (equation (22) above), so  -space is the eigenspace for
-space is the eigenspace for  .
.
Similarly, since position is a measurable quantity for the quantum particle in a ring, there is a position operator  which generates a position measurement space, just as
which generates a position measurement space, just as 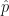 generates momentum measurement space. The eigenvalue equation for
generates momentum measurement space. The eigenvalue equation for  is simply
is simply

Note that each of  and
and 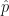 can be expressed in the language of the other’s space. Expressing
can be expressed in the language of the other’s space. Expressing  in
in  -language, we find
-language, we find

(Proof:  ). Similarly, expressing
). Similarly, expressing 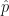 in
in  -language we get
-language we get

(Proof:  ). In each case, we are not using the correct eigenspace for the operator, so the equations we get are not in the form of proper eigenvalue equations. However, we can check that (27) and (28) are correct by seeing if they do produce proper eigenvalue equations when applied to the correct kets. When applied to the ket
). In each case, we are not using the correct eigenspace for the operator, so the equations we get are not in the form of proper eigenvalue equations. However, we can check that (27) and (28) are correct by seeing if they do produce proper eigenvalue equations when applied to the correct kets. When applied to the ket  , equation (27) must produce the proper eigenvalue equation
, equation (27) must produce the proper eigenvalue equation

Therefore we need to confirm that

but this result is immediate when we substitute (12) into each side of (30). Similarly, when applied to the ket  , equation (28) must produce the proper eigenvalue equation
, equation (28) must produce the proper eigenvalue equation

Therefore we need to confirm that

but this is again immediate when we substitute (7) into each side of (32).
Another interesting thing to observe here is that we can reverse this argument and derive the form of the probability amplitude  as a function of
as a function of  from (32), interpreted as a differential equation. We can regard (32) as the the eigenvalue equation in (25) above, but expressed in the language of
from (32), interpreted as a differential equation. We can regard (32) as the the eigenvalue equation in (25) above, but expressed in the language of  (i.e., the differential equation in (32) is obtained by introducing the bra
(i.e., the differential equation in (32) is obtained by introducing the bra  in (25) above, yielding
in (25) above, yielding  ). The solution to (32) is precisely the form of
). The solution to (32) is precisely the form of  given in (7) above, with the constant coming from the normalization condition
given in (7) above, with the constant coming from the normalization condition  as before.
as before.
In addition to position and momentum operators  and
and 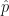 , energy is also an observable, so it must have an operator that generates the spectrum of measurable energies. This is the Hamiltonian operator, which for a quantum particle in a ring model has the form
, energy is also an observable, so it must have an operator that generates the spectrum of measurable energies. This is the Hamiltonian operator, which for a quantum particle in a ring model has the form

(There is no potential energy in our simple model system, so no function of  in the Hamiltonian). Note that the form of the operator
in the Hamiltonian). Note that the form of the operator  is the same as the form of the classical kinetic energy function
is the same as the form of the classical kinetic energy function  . In the quantum case, the eigenvalues of
. In the quantum case, the eigenvalues of  are precisely
are precisely  . Remarkably, a simple rule that works for finding quantum mechanical operators corresponding to classical observables is to put hats on the observables in algebraic relations between classical observables. This is how we can get
. Remarkably, a simple rule that works for finding quantum mechanical operators corresponding to classical observables is to put hats on the observables in algebraic relations between classical observables. This is how we can get  from
from  . As another example, we could in principle obtain a quantum velocity operator as
. As another example, we could in principle obtain a quantum velocity operator as  .
.
Having the form of the Hamiltonian operator  , we can now find its eigenvalues from the eigenvalue problem that generates them:
, we can now find its eigenvalues from the eigenvalue problem that generates them:

This is actually the general form of the famous time-independent Schrödinger equation. Casting this equation into  -space, we can solve for the probability amplitudes
-space, we can solve for the probability amplitudes  :
:

This is a simple second-order linear differential equation with general solution

From the fact that this wave function must be single-valued for our quantum particle in a ring, we deduce

for  . Remember, however, that there is degeneracy in
. Remember, however, that there is degeneracy in 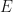 for the quantum particle in a ring model: there is nothing to prevent there being two possible
for the quantum particle in a ring model: there is nothing to prevent there being two possible  -states (one positive, one negative) for each value of
-states (one positive, one negative) for each value of 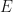 .
.
Quantum particle on an infinite line
Suppose we modify the previous model by allowing the radius of the ring,  , to become infinitely large, so that the `track’ now effectively extends infinitely to the right and infinitely to the left of the starting point at zero. The quantum particle is then free to move anywhere on the real line, i.e., the position measurement space has become
, to become infinitely large, so that the `track’ now effectively extends infinitely to the right and infinitely to the left of the starting point at zero. The quantum particle is then free to move anywhere on the real line, i.e., the position measurement space has become  . For such a quantum particle, momentum is no longer quantized (intuitively, this is because the probability amplitude periodicity constraint
. For such a quantum particle, momentum is no longer quantized (intuitively, this is because the probability amplitude periodicity constraint  is no longer relevant), so the momentum measurement space is now
is no longer relevant), so the momentum measurement space is now  . In this context, with both position and momentum being continuous measurement spaces, Fourier transforms arise naturally because they enable any function of
. In this context, with both position and momentum being continuous measurement spaces, Fourier transforms arise naturally because they enable any function of  over the domain
over the domain  , such as
, such as  , to be expanded as an integral in
, to be expanded as an integral in 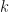 over the same domain:
over the same domain:

where  is given by
is given by

We can use this Fourier transform relationship to obtain physically-realistic mathematical models of a quantum particle on an infinite line. As is well known, in order to obtain a well-behaved wave function representation of a free particle on an infinite line, i.e., a wave function that is square-integrable, it is necessary to construct a superposition of pure waves incorporating a continuous range of wave numbers 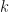 . This wave packet approach then naturally gives rise to discussions relating to Heisenberg’s uncertainty principle. Before considering this, however, it is interesting to note that we can also derive a pseudo-normalized pure wave form for the wave function
. This wave packet approach then naturally gives rise to discussions relating to Heisenberg’s uncertainty principle. Before considering this, however, it is interesting to note that we can also derive a pseudo-normalized pure wave form for the wave function  in the case of a quantum particle on an infinite line, somewhat analogous to the pure wave form in the previous section. To do this, we will first obtain a representation of the Dirac delta function using the above Fourier transform by letting
in the case of a quantum particle on an infinite line, somewhat analogous to the pure wave form in the previous section. To do this, we will first obtain a representation of the Dirac delta function using the above Fourier transform by letting  . Putting this into (38) gives
. Putting this into (38) gives

Then, putting this result into (37) gives us the following useful representation:

We will also observe that for any  , we have
, we have

(To see this, note first that  because
because  . Therefore, only the absolute value of
. Therefore, only the absolute value of 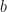 in
in  is relevant. We need to show that
is relevant. We need to show that  . In the integral on the left-hand side, make the change of variable
. In the integral on the left-hand side, make the change of variable  . Then
. Then  and
and  , and noting that
, and noting that  , i.e., both are functions of
, i.e., both are functions of  , we can write
, we can write  as required).
as required).
We now use this machinery to derive an explicit pure wave functional form for  . First, consider the self-space bra-ket
. First, consider the self-space bra-ket

where the final equality follows from (41). Using (40), reversing the roles of  and
and 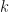 there, we can write
there, we can write



![= \int_{-\infty}^{\infty} dx \big[\frac{1}{\sqrt{h}}\exp(-i k x)\big]\big[\frac{1}{\sqrt{h}} \exp(i K x) \big]\qquad \qquad \qquad \qquad \qquad (43)](https://s0.wp.com/latex.php?latex=%3D+%5Cint_%7B-%5Cinfty%7D%5E%7B%5Cinfty%7D+dx+%5Cbig%5B%5Cfrac%7B1%7D%7B%5Csqrt%7Bh%7D%7D%5Cexp%28-i+k+x%29%5Cbig%5D%5Cbig%5B%5Cfrac%7B1%7D%7B%5Csqrt%7Bh%7D%7D+%5Cexp%28i+K+x%29+%5Cbig%5D%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2843%29&bg=ffffff&fg=111111&s=0&c=20201002)
But we also have in Dirac notation

Comparing (43) and (44) we can immediately see that

The only difference between  here and in (7) above for the quantum particle in a ring case is that the normalization constant here is
here and in (7) above for the quantum particle in a ring case is that the normalization constant here is  instead of
instead of  . It is easily checked that (45) is in fact not square-integrable for the case of the quantum particle on an infinite line, i.e.,
. It is easily checked that (45) is in fact not square-integrable for the case of the quantum particle on an infinite line, i.e.,  is not an element of a Hilbert space in the conventional way here, since
is not an element of a Hilbert space in the conventional way here, since  . Instead, a kind of pseudo-normalization convention is being used in specifying the normalization constant in (45), called normalization to a Dirac delta function. From (43) (remembering that
. Instead, a kind of pseudo-normalization convention is being used in specifying the normalization constant in (45), called normalization to a Dirac delta function. From (43) (remembering that  ) we see that the normalization constant in (45) is giving us normalization to a Dirac delta function in the form
) we see that the normalization constant in (45) is giving us normalization to a Dirac delta function in the form

However, the non-square-integrable individual pure waves in (45) do not represent physically realizable states. To construct a square-integrable wave packet representation of a quantum particle on a line, we go back to the Fourier transform equation (37) above and regard it as a sum of pure waves over a continuous range of wave numbers 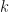 , with the amplitudes of these pure waves being modulated by the function
, with the amplitudes of these pure waves being modulated by the function  . A standard example is a Gaussian wave packet which we can obtain here by specifying
. A standard example is a Gaussian wave packet which we can obtain here by specifying

where  is some fixed wave number. Note that
is some fixed wave number. Note that  is the probability density function of a
is the probability density function of a  variable, i.e., up to a normalizing constant we get a Gaussian probability distribution for the wave number
variable, i.e., up to a normalizing constant we get a Gaussian probability distribution for the wave number 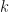 centered on
centered on  with standard deviation
with standard deviation  . Inserting this expression for
. Inserting this expression for  in (37) gives
in (37) gives

The integral here can be solved using straightforward changes of variables to give the result

This is a localized wave function and is square-integrable since  is the probability density function of a
is the probability density function of a  variable, i.e., we get a Gaussian probability distribution for the position
variable, i.e., we get a Gaussian probability distribution for the position  centered at zero and with standard deviation
centered at zero and with standard deviation  . (As a check, note that substituting this expression for
. (As a check, note that substituting this expression for  into (38) must give us the expression we used for
into (38) must give us the expression we used for  . Using the the result
. Using the the result

and the fact that  , we can substitute the expression for
, we can substitute the expression for  into (38) to get
into (38) to get





as required). Denoting the standard deviation of  by
by  and the standard deviation of
and the standard deviation of 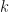 by
by  , we have
, we have

But using  , we can write this as
, we can write this as

It can be shown that for anything other than a Gaussian wave packet we would find

and thus we obtain the famous Heisenberg uncertainty principle for position and momentum:

This wave packet model is a static one, i.e., the wave function  is time-independent. We can obtain a time-dependent wave function
is time-independent. We can obtain a time-dependent wave function  by multiplying the integrand in (37) by a quantum mechanical time evolution operator (the time evolution operator will be discussed below). Then, using the same
by multiplying the integrand in (37) by a quantum mechanical time evolution operator (the time evolution operator will be discussed below). Then, using the same  as in the static case and manipulating the integral in a similar manner as before, we find that
as in the static case and manipulating the integral in a similar manner as before, we find that  is again a localized Gaussian wave packet but now with the property that the standard deviation of the associated Gaussian probability distribution increases with time (i.e., the bell-shaped Gaussian probability distribution spreads out over time).
is again a localized Gaussian wave packet but now with the property that the standard deviation of the associated Gaussian probability distribution increases with time (i.e., the bell-shaped Gaussian probability distribution spreads out over time).
Quantum harmonic oscillator
To extend the model further, we now consider a quantum harmonic oscillator in which the position still has domain  . In this model, the momentum
. In this model, the momentum  is again no longer quantized but energy
is again no longer quantized but energy 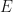 remains quantized and is no longer a degenerate measurement. The approach is essentially to take the ideal classical harmonic oscillator’s Hamiltonian, convert it to a quantum mechanical Hamiltonian operator by `putting hats’ on the classical observables, and then use the operator to solve an eigenvalue problem.
remains quantized and is no longer a degenerate measurement. The approach is essentially to take the ideal classical harmonic oscillator’s Hamiltonian, convert it to a quantum mechanical Hamiltonian operator by `putting hats’ on the classical observables, and then use the operator to solve an eigenvalue problem.
Recall that, in the ideal classical harmonic oscillator model, a particle of mass  attached to a spring with spring constant
attached to a spring with spring constant 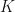 is always pulled towards an equilibrium position by a Hooke’s law force
is always pulled towards an equilibrium position by a Hooke’s law force  . Newton’s second law
. Newton’s second law 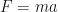 then gives us a second-order differential equation
then gives us a second-order differential equation

with general solution

The angular frequency (or, equivalently, angular velocity – radians per second) is thus

and is usually referred to as the natural oscillation frequency of the harmonic oscillator.
The particle’s kinetic energy is  where
where  is the classical linear momentum, and, unlike the previous models, we now have a potential energy
is the classical linear momentum, and, unlike the previous models, we now have a potential energy  . (Recall that potential energy is the negative of work,
. (Recall that potential energy is the negative of work, 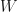 . For the classical harmonic oscillator, we have
. For the classical harmonic oscillator, we have  , so the potential energy is the negative of this). The classical Hamiltonian is then
, so the potential energy is the negative of this). The classical Hamiltonian is then

Using (49), we can write the corresponding quantum mechanical Hamiltonian operator as

As before, the position spectrum is generated by  and the momentum spectrum is generated by
and the momentum spectrum is generated by 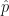 . The energy spectrum is generated by
. The energy spectrum is generated by  via the time-independent Schrödinger equation, which is the following eigenvalue problem for
via the time-independent Schrödinger equation, which is the following eigenvalue problem for 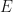 :
:

In Dirac notation, this general eigenvalue problem statement does not yet specify a `language’ in which to express the solutions. We can cast the eigenvalue problem into  -space by introducing the bra
-space by introducing the bra  and expressing the operator
and expressing the operator  in
in  -language. We get the time-independent Schrödinger equation as the second-order differential equation
-language. We get the time-independent Schrödinger equation as the second-order differential equation

This is a well-known differential equation in disguise. The general form is

It is easily seen that (53) becomes (54) if we take

and

The solutions of (54) are stated in terms of the Hermite polynomials,  ,
,  ,
,  ,
,  . The solutions in terms of
. The solutions in terms of  are
are

where only solutions with nonnegative integer values of 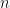 make
make  square-integrable, so only these solutions are allowable. We see that
square-integrable, so only these solutions are allowable. We see that 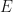 is indeed quantized, i.e., indexed by nonnegative integers
is indeed quantized, i.e., indexed by nonnegative integers 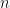 , so if we wanted to we could write
, so if we wanted to we could write  as
as  to emphasise the relevant energy index. The
to emphasise the relevant energy index. The  sequence of energies means that
sequence of energies means that 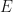 can never be zero for the quantum harmonic oscillator, and it can only go up in discrete steps of
can never be zero for the quantum harmonic oscillator, and it can only go up in discrete steps of  from its minimum value of
from its minimum value of  . Also note that, as stated earlier, the ladder of
. Also note that, as stated earlier, the ladder of 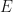 values is not degenerate for the quantum harmonic oscillator (unlike the particle in a ring model) because only nonnegative integers
values is not degenerate for the quantum harmonic oscillator (unlike the particle in a ring model) because only nonnegative integers 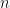 yield valid solutions for this particular eigenvalue problem.
yield valid solutions for this particular eigenvalue problem.
The quantum harmonic oscillator is also used to introduce additional quantum concepts such as quantum tunnelling (the probability amplitudes  are nonzero outside the quadratic potential well for this model, so there is a nonzero probability that the quantum particle can be found outside the potential well. This would be impossible for the classical harmonic oscillator). Another thing to observe here is that it is also possible to cast the eigenvalue problem in
are nonzero outside the quadratic potential well for this model, so there is a nonzero probability that the quantum particle can be found outside the potential well. This would be impossible for the classical harmonic oscillator). Another thing to observe here is that it is also possible to cast the eigenvalue problem in  -language instead of
-language instead of  -language (resulting in expressions for the probability amplitudes
-language (resulting in expressions for the probability amplitudes  which are isomorphic to those for
which are isomorphic to those for  ), and in energy-level language, which introduces the ideas of creation and annihilation operators (also known as raising and lowering operators, respectively, or as ladder operators), as well as commutators. These are nonphysical operators, i.e., they do not correspond to observables, but rather are regarded as useful computational aids.
), and in energy-level language, which introduces the ideas of creation and annihilation operators (also known as raising and lowering operators, respectively, or as ladder operators), as well as commutators. These are nonphysical operators, i.e., they do not correspond to observables, but rather are regarded as useful computational aids.
The annihilation operator  for the quantum harmonic oscillator can be defined in terms of
for the quantum harmonic oscillator can be defined in terms of 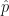 and
and  as
as

and the creation operator is its hermitian conjugate

These can be derived from the Hamiltonian operator by pseudo-factorising it. See my previous note about this. From these two equations, we can show that their commutator is unity, i.e.,
![[\hat{a}, \hat{a}^{\dag}] = \hat{a} \hat{a}^\dag - \hat{a}^{\dag} \hat{a} = 1 \qquad \qquad \qquad \qquad \qquad (60)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Ba%7D%2C+%5Chat%7Ba%7D%5E%7B%5Cdag%7D%5D+%3D+%5Chat%7Ba%7D+%5Chat%7Ba%7D%5E%5Cdag+-+%5Chat%7Ba%7D%5E%7B%5Cdag%7D+%5Chat%7Ba%7D+%3D+1+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2860%29&bg=ffffff&fg=111111&s=0&c=20201002)
and the Hamiltonian operator itself can now be re-expressed in terms of these ladder operators as

We also find
![[\hat{a}, \hat{H}] = \hbar \omega \hat{a} \qquad \qquad \qquad \qquad \qquad (62)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Ba%7D%2C+%5Chat%7BH%7D%5D+%3D+%5Chbar+%5Comega+%5Chat%7Ba%7D+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2862%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{a}^{\dag}, \hat{H}] = -\hbar \omega \hat{a}^{\dag} \qquad \qquad \qquad \qquad \qquad (63)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Ba%7D%5E%7B%5Cdag%7D%2C+%5Chat%7BH%7D%5D+%3D+-%5Chbar+%5Comega+%5Chat%7Ba%7D%5E%7B%5Cdag%7D+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2863%29&bg=ffffff&fg=111111&s=0&c=20201002)
These results allow us to avoid all mention of 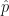 and
and  when investigating the energy measurement space generated by the operator
when investigating the energy measurement space generated by the operator  in the eigenvalue problem given as equation (52) above. We have
in the eigenvalue problem given as equation (52) above. We have
![[\hat{a}, \hat{H}] | E \rangle = \hbar \omega \hat{a} | E \rangle](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Ba%7D%2C+%5Chat%7BH%7D%5D+%7C+E+%5Crangle+%3D+%5Chbar+%5Comega+%5Chat%7Ba%7D+%7C+E+%5Crangle&bg=ffffff&fg=111111&s=0&c=20201002)
and thus

so

Similarly, from
![[\hat{a}^{\dag}, \hat{H}] | E \rangle = -\hbar \omega \hat{a}^{\dag} | E \rangle](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Ba%7D%5E%7B%5Cdag%7D%2C+%5Chat%7BH%7D%5D+%7C+E+%5Crangle+%3D+-%5Chbar+%5Comega+%5Chat%7Ba%7D%5E%7B%5Cdag%7D+%7C+E+%5Crangle&bg=ffffff&fg=111111&s=0&c=20201002)
we have

and so

Therefore,  applied to
applied to  produces a new eigenket
produces a new eigenket  which is lowered in energy by
which is lowered in energy by  . Similarly,
. Similarly,  produces an eigenket raised in energy by
produces an eigenket raised in energy by  . As mentioned earlier, we can use the integer index
. As mentioned earlier, we can use the integer index 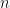 to label the energy states instead of
to label the energy states instead of 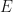 , i.e., we can write
, i.e., we can write  instead of
instead of  . To make the ladder effect of the creation and annihilation operators even more obvious, we can then write
. To make the ladder effect of the creation and annihilation operators even more obvious, we can then write


and try to work out the eigenvalues  and
and  . The value of
. The value of  can be deduced by noting that applying
can be deduced by noting that applying  in the form of (61) above to
in the form of (61) above to  and using (55) we get
and using (55) we get

which reduces to

But  , so we must have
, so we must have  . Therefore (66) can be written explicitly as
. Therefore (66) can be written explicitly as

We now use this result to deduce the value of  by writing it as
by writing it as

Adding a bra  gives us a self-space bracket on the right-hand side:
gives us a self-space bracket on the right-hand side:

But  , so for (68) to be nonzero we must have
, so for (68) to be nonzero we must have  , so
, so  , and notice that this must also be true for
, and notice that this must also be true for  to be nonzero, so
to be nonzero, so  and
and  must both represent the same function. With these insights, we can re-express (68) as
must both represent the same function. With these insights, we can re-express (68) as

Taking the hermitian conjugate of both sides of (69) gives

from which we deduce that the explicit form of (67) must be

i.e.,  . Thus, we have
. Thus, we have


Quantum particle on a spherical shell
We now extend the model further by introducing two-dimensional quantum states for a quantum particle on a spherical shell. The general approach to modelling is similar to the approach for the harmonic oscillator in a number of ways. In particular, we begin by setting up a classical model of a particle on a sphere, and then quantize it by considering the relevant quantum mechanical operators in a quantum version of the model.
In a classical model of a particle on a spherical shell, the particle is constrained to positions at a fixed distance 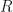 from the origin, but can otherwise move anywhere on a spherical surface. In the previous quantum particle in a ring model,
from the origin, but can otherwise move anywhere on a spherical surface. In the previous quantum particle in a ring model,  was assumed to be sufficiently large to enable angular momentum considerations to be ignored, and the focus was then on linear momentum
was assumed to be sufficiently large to enable angular momentum considerations to be ignored, and the focus was then on linear momentum  . In the present particle on a spherical shell model, we no longer assume
. In the present particle on a spherical shell model, we no longer assume 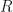 is large and in fact the particle now only has angular momentum. As discussed in a previous post involving angular momentum calculations, the classical particle has a vector angular momentum about the origin given by
is large and in fact the particle now only has angular momentum. As discussed in a previous post involving angular momentum calculations, the classical particle has a vector angular momentum about the origin given by

which has components



There is no potential energy in this model, only kinetic energy, but the constraint that the particle must remain on the spherical shell means that  and
and  are always orthogonal, so
are always orthogonal, so

This linear constraint means that only two of the three linear momentum components are linearly independent, so the linear momentum space for this model is two-dimensional. In view of (71) and (75), the magnitudes of the linear and angular momentum are related by

so

Therefore, the Hamiltonian for the classical particle in a shell model is

Using spherical coordinates, the classical particle can wander anywhere on the sphere, with any angular momentum in any direction, its position characterised by the polar angle 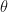 and the azimuthal angle
and the azimuthal angle  . In the case of a quantum particle on a spherical shell, a position measurement defines a two-dimensional basis space and a position state would be denoted by the ket
. In the case of a quantum particle on a spherical shell, a position measurement defines a two-dimensional basis space and a position state would be denoted by the ket  . There would be two quantum operators
. There would be two quantum operators  and
and  whose eigenvalues are the spectra of possible
whose eigenvalues are the spectra of possible 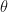 and
and  values respectively, and a single eigenstate
values respectively, and a single eigenstate  is now regarded as a simultaneous solution of the two eigenvalue problems for these operators:
is now regarded as a simultaneous solution of the two eigenvalue problems for these operators:


This is possible if and only if  and
and  commute, i.e.,
commute, i.e., ![[\hat{\theta}, \hat{\varphi}] = 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7B%5Ctheta%7D%2C+%5Chat%7B%5Cvarphi%7D%5D+%3D+0&bg=ffffff&fg=111111&s=0&c=20201002) . Operators which commute are called compatible operators and they must have simultaneous eigenstates. Conversely, two operators which have simultaneous eigenstates must commute. (An indication of why this is true is as follows. Suppose we are given the eigenvalue equation (78), so that
. Operators which commute are called compatible operators and they must have simultaneous eigenstates. Conversely, two operators which have simultaneous eigenstates must commute. (An indication of why this is true is as follows. Suppose we are given the eigenvalue equation (78), so that  is an eigenstate of
is an eigenstate of  with eigenvalue
with eigenvalue 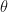 . Then, given
. Then, given ![[\hat{\theta}, \hat{\varphi}] = 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7B%5Ctheta%7D%2C+%5Chat%7B%5Cvarphi%7D%5D+%3D+0&bg=ffffff&fg=111111&s=0&c=20201002) , we must have
, we must have

Therefore, both  and
and  are eigenstates of
are eigenstates of  with the same eigenvalue
with the same eigenvalue 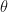 , so they must represent the same eigenstate up to some proportionality constant. The fact that
, so they must represent the same eigenstate up to some proportionality constant. The fact that  and
and  represent the same eigenstate up to a proportionality constant is exactly what (79) says). The fact that this condition holds means that the measurement of an eigenvalue of
represent the same eigenstate up to a proportionality constant is exactly what (79) says). The fact that this condition holds means that the measurement of an eigenvalue of  does not destroy knowledge of an eigenvalue of
does not destroy knowledge of an eigenvalue of  , and vice versa. This is not possible with all pairs of measurements. For example, the operators
, and vice versa. This is not possible with all pairs of measurements. For example, the operators  and
and 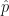 are incompatible and thus do not have simultaneous eigenstates, so no two-dimensional state such as
are incompatible and thus do not have simultaneous eigenstates, so no two-dimensional state such as  exists. Knowledge of
exists. Knowledge of  would be destroyed by a measurement of
would be destroyed by a measurement of  , and vice versa. This is indicated by the fact that
, and vice versa. This is indicated by the fact that  and
and 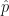 do not commute, since
do not commute, since ![[\hat{x}, \hat{p}] = i \hbar \neq 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Bx%7D%2C+%5Chat%7Bp%7D%5D+%3D+i+%5Chbar+%5Cneq+0&bg=ffffff&fg=111111&s=0&c=20201002) . Simultaneous eigenstates can only exist for operators which commute.
. Simultaneous eigenstates can only exist for operators which commute.
Note that this idea of compatible vs incompatible operators is intimately related to Heisenberg’s uncertainty principle. Given two operators  and
and  , with standard deviations
, with standard deviations  and
and  respectively, the generalised form of Heisenberg’s uncertainty principle says
respectively, the generalised form of Heisenberg’s uncertainty principle says
![\Delta a \Delta b \ge \frac{1}{2} |\langle [\hat{A}, \hat{B}] \rangle|](https://s0.wp.com/latex.php?latex=%5CDelta+a+%5CDelta+b+%5Cge+%5Cfrac%7B1%7D%7B2%7D+%7C%5Clangle+%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D+%5Crangle%7C&bg=ffffff&fg=111111&s=0&c=20201002)
where ![|\langle [\hat{A}, \hat{B}] \rangle|](https://s0.wp.com/latex.php?latex=%7C%5Clangle+%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D+%5Crangle%7C&bg=ffffff&fg=111111&s=0&c=20201002) denotes the absolute value of the expectation of the commutator of
denotes the absolute value of the expectation of the commutator of  and
and  . (The concept of the expectation of an operator is discussed in a later section below). Thus, there is no uncertainty principle for compatible operators, and measurement of one will not affect measurement of the other. However, there is always an uncertainty principle for incompatible operators, i.e., those with non-zero commutators, and it is impossible to measure one without destroying a previous measurement of the other.
. (The concept of the expectation of an operator is discussed in a later section below). Thus, there is no uncertainty principle for compatible operators, and measurement of one will not affect measurement of the other. However, there is always an uncertainty principle for incompatible operators, i.e., those with non-zero commutators, and it is impossible to measure one without destroying a previous measurement of the other.
Recall that in the case of the harmonic oscillator we could solve the eigenvalue problem in  -language,
-language,  -language, or energy-level-language, and the energy-level-language approach gave rise to creation and annihilation operator approaches. Similar considerations apply to the quantum particle on a spherical shell model. We can solve the eigenvalue problem in the language of angular momentum components rather than in the language of spatial or linear momentum states, and this gives rise to ladder operators analogous to the creation and annihilation operators for the quantum harmonic oscillator. Since angular momentum components can be measured, there must be angular momentum state labels and angular momentum operators. The angular momentum operators are simply the classical angular momenta turned into operators by `putting hats on them’. Thus, we get the operators
-language, or energy-level-language, and the energy-level-language approach gave rise to creation and annihilation operator approaches. Similar considerations apply to the quantum particle on a spherical shell model. We can solve the eigenvalue problem in the language of angular momentum components rather than in the language of spatial or linear momentum states, and this gives rise to ladder operators analogous to the creation and annihilation operators for the quantum harmonic oscillator. Since angular momentum components can be measured, there must be angular momentum state labels and angular momentum operators. The angular momentum operators are simply the classical angular momenta turned into operators by `putting hats on them’. Thus, we get the operators




The eigenvalues of  make up the measurement spectrum of the square of the total angular momentum.
make up the measurement spectrum of the square of the total angular momentum.
We know that spatial states  and linear momentum states are two-dimensional, so we must also find that the measurement space created by the angular momentum operators is two-dimensional since dimensionality is conserved, no matter what language is used to describe the system. Indeed, we find that no two of the three angular momentum operators commute with each other:
and linear momentum states are two-dimensional, so we must also find that the measurement space created by the angular momentum operators is two-dimensional since dimensionality is conserved, no matter what language is used to describe the system. Indeed, we find that no two of the three angular momentum operators commute with each other:
![[\hat{L}_x, \hat{L}_y] = i\hbar \hat{L}_z \qquad \qquad \qquad \qquad \qquad (84)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_x%2C+%5Chat%7BL%7D_y%5D+%3D+i%5Chbar+%5Chat%7BL%7D_z+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2884%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{L}_y, \hat{L}_z] = i\hbar \hat{L}_x \qquad \qquad \qquad \qquad \qquad (85)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_y%2C+%5Chat%7BL%7D_z%5D+%3D+i%5Chbar+%5Chat%7BL%7D_x+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2885%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{L}_z, \hat{L}_x] = i\hbar \hat{L}_y \qquad \qquad \qquad \qquad \qquad (86)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_z%2C+%5Chat%7BL%7D_x%5D+%3D+i%5Chbar+%5Chat%7BL%7D_y+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2886%29&bg=ffffff&fg=111111&s=0&c=20201002)
Therefore, it is impossible to define eigenstates based on these components. However, all three components do commute with  :
:
![[\hat{L}_x, \hat{L}^2] = [\hat{L}_y, \hat{L}^2] = [\hat{L}_z, \hat{L}^2] = 0 \qquad \qquad \qquad \qquad \qquad (87)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_x%2C+%5Chat%7BL%7D%5E2%5D+%3D+%5B%5Chat%7BL%7D_y%2C+%5Chat%7BL%7D%5E2%5D+%3D+%5B%5Chat%7BL%7D_z%2C+%5Chat%7BL%7D%5E2%5D+%3D+0+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2887%29&bg=ffffff&fg=111111&s=0&c=20201002)
Therefore, it is possible to characterise an eigenstate using  and any one of the components. In what follows, we will use a basis corresponding to the simultaneous eigenstates of
and any one of the components. In what follows, we will use a basis corresponding to the simultaneous eigenstates of  and
and  . Suppose the eigenvalues of
. Suppose the eigenvalues of  are
are  and the eigenvalues of
and the eigenvalues of  are
are  (
( has dimensions of angular momentum, so its presence here enables
has dimensions of angular momentum, so its presence here enables  and
and 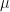 to be treated as dimensionless). We now seek to find
to be treated as dimensionless). We now seek to find  and
and 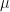 as simultaneous solutions of the two eigenvalue problems
as simultaneous solutions of the two eigenvalue problems


To do this, we define two new operators, the lowering and raising operators  and
and  , which are the analogues of the annihilation and creation operators for the harmonic oscillator:
, which are the analogues of the annihilation and creation operators for the harmonic oscillator:


Note that since  commutes with
commutes with  and
and  , it must also commute with
, it must also commute with  and
and  . We find that
. We find that
![[\hat{L}_{-}, \hat{L}_z] = \hbar \hat{L}_{-} \qquad \qquad \qquad \qquad \qquad (92)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_%7B-%7D%2C+%5Chat%7BL%7D_z%5D+%3D+%5Chbar+%5Chat%7BL%7D_%7B-%7D+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2892%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{L}_z, \hat{L}_{+}] = \hbar \hat{L}_{+} \qquad \qquad \qquad \qquad \qquad (93)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D_z%2C+%5Chat%7BL%7D_%7B%2B%7D%5D+%3D+%5Chbar+%5Chat%7BL%7D_%7B%2B%7D+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2893%29&bg=ffffff&fg=111111&s=0&c=20201002)
and also
![[\hat{L}^2, \hat{L}_{-}] = [\hat{L}^2, \hat{L}_{+}] = 0 \qquad \qquad \qquad \qquad \qquad (94)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BL%7D%5E2%2C+%5Chat%7BL%7D_%7B-%7D%5D+%3D+%5B%5Chat%7BL%7D%5E2%2C+%5Chat%7BL%7D_%7B%2B%7D%5D+%3D+0+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%2894%29&bg=ffffff&fg=111111&s=0&c=20201002)
Following a similar line of reasoning as with the annihilation and creation operators of the quantum harmonic oscillator, we find that


To find  and
and  , we begin by noting that
, we begin by noting that  since
since  is just one component of
is just one component of  . Therefore,
. Therefore, 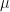 is bounded, so there must be a
is bounded, so there must be a  and a
and a  . Let
. Let  . Next, we observe that the existence of the ladder operators in (95) and (96) implies that the eigenvalues
. Next, we observe that the existence of the ladder operators in (95) and (96) implies that the eigenvalues 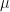 are discrete, consisting of a ladder of unit steps. Thus, we have
are discrete, consisting of a ladder of unit steps. Thus, we have

for some 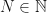 , and therefore
, and therefore

We next observe that


because the minimum state cannot be lowered further and the maximum state cannot be raised further. We also observe that  can be expressed in terms of
can be expressed in terms of  and
and  in two different ways:
in two different ways:


We now apply (100) to the state  , using (98), (88) and (89), and we get
, using (98), (88) and (89), and we get

Similarly, applying (101) to the state  using (99) we get
using (99) we get

From (102) and (103) we get

which implies

We conclude from (103) and (104) that  in (88), where the allowed spectrum of
in (88), where the allowed spectrum of 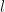 values are the nonnegative half-integers:
values are the nonnegative half-integers:

And 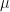 runs from
runs from  to
to  in integer steps. Using these results in (88) and (89), and using
in integer steps. Using these results in (88) and (89), and using 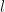 to label an eigenstate of
to label an eigenstate of  instead of
instead of  , we conclude
, we conclude


where  is an integer and
is an integer and 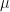 runs from
runs from  to
to 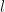 in integer steps:
in integer steps:

Finally, to find  in (95), we apply (100) to the state
in (95), we apply (100) to the state  to get
to get

which implies

Taking  to be real, we get
to be real, we get

and

Therefore, the effects of the lowering and raising operators are


So far, we have worked out the quantum particle in a spherical shell model using the language of angular momentum,  . We can also use the language of position,
. We can also use the language of position,  , and in fact we can work out the transformation matrix elements
, and in fact we can work out the transformation matrix elements  which also have the physical interpretation of being probability amplitudes for finding the quantum particle at position
which also have the physical interpretation of being probability amplitudes for finding the quantum particle at position  when it is known to be in angular momentum state
when it is known to be in angular momentum state  . This exercise will reveal the crucial fact that
. This exercise will reveal the crucial fact that 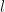 in (105) can only take integer values in the case of orbital angular momentum.
in (105) can only take integer values in the case of orbital angular momentum.
We first of all cast (106) and (107) in the language of  by introducing a bra
by introducing a bra  :
:


To implement these equations, we need  and
and  , i.e., we need the operators
, i.e., we need the operators  and
and  expressed in the language of
expressed in the language of  . I obtained these expressions as well as expressions for
. I obtained these expressions as well as expressions for  and
and  in a previous post. We can also use these to get expressions for
in a previous post. We can also use these to get expressions for  and
and  . Using
. Using

in (112) we get a differential equation

And using

in (111) we get a second differential equation

The transformation matrix elements  are the simultaneous solutions of these two differential equations. From (113) we deduce that
are the simultaneous solutions of these two differential equations. From (113) we deduce that

where  is some function of
is some function of 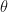 . This equation is crucial because it reveals that
. This equation is crucial because it reveals that 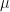 can only take integer values. This is a necessary condition for
can only take integer values. This is a necessary condition for  to be periodic with respect to
to be periodic with respect to  , which it must be. But by (108) this in turn implies that
, which it must be. But by (108) this in turn implies that 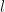 can only take integer values in the case of orbital angular momentum. The half-integer values in (105) must relate to something other than orbital angular momentum and will be found below to correspond to quantum mechanical spin angular momentum.
can only take integer values in the case of orbital angular momentum. The half-integer values in (105) must relate to something other than orbital angular momentum and will be found below to correspond to quantum mechanical spin angular momentum.
Using (115) in (114) we get a well-known differential equation:

This is satisfied by the associated Legendre polynomials,  . These are the functions
. These are the functions  in (115). Using
in (115). Using  to construct properly normalized simultaneous solutions to (113) and (114) we obtain finally
to construct properly normalized simultaneous solutions to (113) and (114) we obtain finally

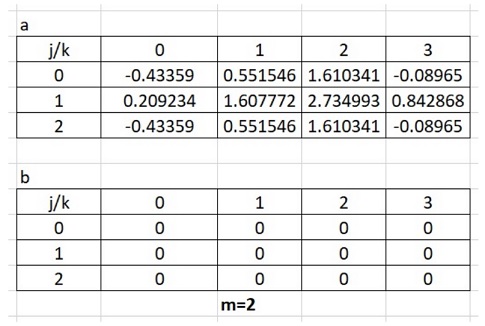
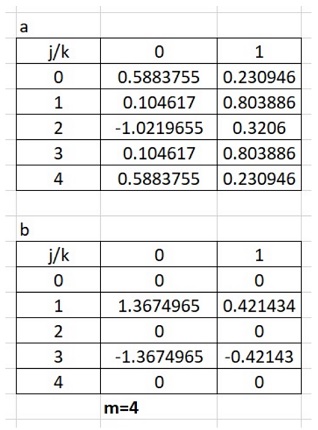
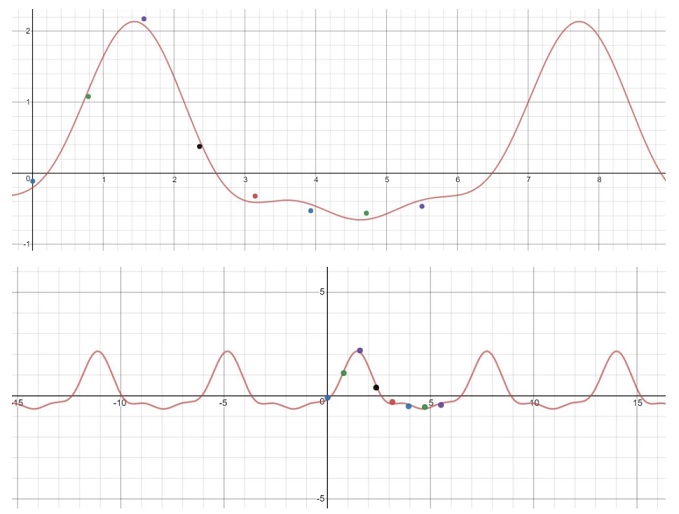
where the functions  are well-known tabulated functions called the spherical harmonic functions. Interestingly, these functions characterise the normal mode standing waves of the vibrations of a spherical shell, i.e., the fundamental and all the harmonics of a spherical drumhead. They are the two-dimensional analogues on a sphere of one-dimensional sines and cosines (the harmonic functions for a line). The correct normalization constants for the probability amplitudes in (117) would be found using the certainty condition, which in spherical coordinates is
are well-known tabulated functions called the spherical harmonic functions. Interestingly, these functions characterise the normal mode standing waves of the vibrations of a spherical shell, i.e., the fundamental and all the harmonics of a spherical drumhead. They are the two-dimensional analogues on a sphere of one-dimensional sines and cosines (the harmonic functions for a line). The correct normalization constants for the probability amplitudes in (117) would be found using the certainty condition, which in spherical coordinates is

Spin, Pauli spin matrices and matrix mechanics
The angular momentum of a circulating charged particle gives rise to a magnetic dipole moment. This concept is usually first encountered in elementary electromagnetism when considering the torque on a current loop immersed a magnetic field  , which is given by
, which is given by

where

is the magnetic dipole moment. Here, 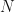 is the number of turns in the current loop,
is the number of turns in the current loop,  is the conventional current flowing through the loop (i.e., the rate at which positive charge is flowing through a cross-section of the conducting loop),
is the conventional current flowing through the loop (i.e., the rate at which positive charge is flowing through a cross-section of the conducting loop),  is the area enclosed by the current loop and
is the area enclosed by the current loop and  is a unit vector which is normal to the plane of the area
is a unit vector which is normal to the plane of the area  in the sense given by the right-hand rule. (The direction of the normal unit vector would be the reverse of that indicated by the right-hand rule if a negative charge flow was being considered).
in the sense given by the right-hand rule. (The direction of the normal unit vector would be the reverse of that indicated by the right-hand rule if a negative charge flow was being considered).
In the case of a classical charged particle of mass  and positive charge
and positive charge  circulating around a spherical shell of radius
circulating around a spherical shell of radius 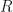 with speed
with speed  , we have
, we have  ,
,  ,
,  , and
, and  , so the magnitude of the magnetic dipole moment is obtained as
, so the magnitude of the magnetic dipole moment is obtained as

where  and
and 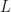 are the magnitudes of the linear and angular momenta of the orbiting charged particle respectively. In vector form, we have
are the magnitudes of the linear and angular momenta of the orbiting charged particle respectively. In vector form, we have

where the vectors point in a direction given by the right-hand rule. Thus, we see that the magnetic dipole moment is directly proportional to the angular momentum of the orbiting charged particle, with the constant of proportionality involving the charge-to-mass ratio of the particle.
Based on the link between magnetic dipole moment and angular momentum exhibited in (121), we would expect that the magnetic dipole moment of a quantum charged particle, e.g., an electron, say in the  -direction of a coordinate system, would be related to the operators
-direction of a coordinate system, would be related to the operators  and
and  in (106) and (107) above with their discrete spectra of eigenvalues. This is indeed the case. The iconic Stern-Gerlach experiment of 1922 was designed to measure the magnetic dipole moments of quantum particles and indeed found that these were quantized in accordance with the relationship suggested by (121) and the operators
in (106) and (107) above with their discrete spectra of eigenvalues. This is indeed the case. The iconic Stern-Gerlach experiment of 1922 was designed to measure the magnetic dipole moments of quantum particles and indeed found that these were quantized in accordance with the relationship suggested by (121) and the operators  and
and  discussed in the previous section. For example, the Stern-Gerlach apparatus produced discrete line spectra when measuring the
discussed in the previous section. For example, the Stern-Gerlach apparatus produced discrete line spectra when measuring the  component of magnetic dipole moment, rather than continuous spectra which would have been expected classically, with the multiplicities of the discrete line spectra corresponding exactly to the multiplicities of the eigenvalues
component of magnetic dipole moment, rather than continuous spectra which would have been expected classically, with the multiplicities of the discrete line spectra corresponding exactly to the multiplicities of the eigenvalues 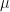 in (108) for given values of
in (108) for given values of 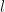 . In other words, for any given value of
. In other words, for any given value of 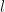 , the multiplicity of the discrete line spectra produced by the Stern-Gerlach apparatus was
, the multiplicity of the discrete line spectra produced by the Stern-Gerlach apparatus was  in accordance with (108).
in accordance with (108).
It was noted in the previous section that 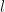 can only take integer values in the case of orbital angular momentum, so if magnetic dipole moments were due only to orbital angular momentum the multiplicities
can only take integer values in the case of orbital angular momentum, so if magnetic dipole moments were due only to orbital angular momentum the multiplicities  of the discrete line spectra produced by the Stern-Gerlach apparatus would always be odd numbers. However, this is not what was observed. Famously, a two-line spectrum was produced for the magnetic dipole moment of a beam of free electrons which had no orbital angular momentum at all. The two-line spectrum corresponded to eigenvalues
of the discrete line spectra produced by the Stern-Gerlach apparatus would always be odd numbers. However, this is not what was observed. Famously, a two-line spectrum was produced for the magnetic dipole moment of a beam of free electrons which had no orbital angular momentum at all. The two-line spectrum corresponded to eigenvalues 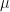 in (108) of
in (108) of 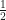 and
and  , and this is only possible if
, and this is only possible if  . Eventually, this result came to be understood as signifying that electrons have an intrinsic spin angular momentum which also produces its own magnetic dipole moment quite distinct from any magnetic moment due to orbital angular momentum. The difference between them is that while it is possible to have nonzero probability amplitudes
. Eventually, this result came to be understood as signifying that electrons have an intrinsic spin angular momentum which also produces its own magnetic dipole moment quite distinct from any magnetic moment due to orbital angular momentum. The difference between them is that while it is possible to have nonzero probability amplitudes  for orbital angular momentum with integer values of
for orbital angular momentum with integer values of 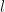 , such probability amplitudes must always be zero for spin angular momentum with
, such probability amplitudes must always be zero for spin angular momentum with 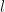 equal to a half-integer. Spin angular momentum simply has no representation in real physical space, so spin states cannot be cast into
equal to a half-integer. Spin angular momentum simply has no representation in real physical space, so spin states cannot be cast into  language.
language.
The convention is to use the letter  rather than
rather than 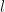 to denote spin parameter values, and we always have
to denote spin parameter values, and we always have  in the case of the electron (we say the electron spin quantum number is
in the case of the electron (we say the electron spin quantum number is 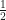 ). Apart from this, however, spin angular momentum operators obey exactly the same rules that were outlined for angular momentum in the previous section. We have a spin vector
). Apart from this, however, spin angular momentum operators obey exactly the same rules that were outlined for angular momentum in the previous section. We have a spin vector  from whose components the operators
from whose components the operators  ,
,  and
and  are built, exactly like
are built, exactly like  and the operators
and the operators  ,
,  and
and  . Also, by (84)-(87) above we have
. Also, by (84)-(87) above we have
![[\hat{S}_x, \hat{S}_y] = i\hbar \hat{S}_z \qquad \qquad \qquad \qquad \qquad (122)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BS%7D_x%2C+%5Chat%7BS%7D_y%5D+%3D+i%5Chbar+%5Chat%7BS%7D_z+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28122%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{S}_y, \hat{S}_z] = i\hbar \hat{S}_x \qquad \qquad \qquad \qquad \qquad (123)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BS%7D_y%2C+%5Chat%7BS%7D_z%5D+%3D+i%5Chbar+%5Chat%7BS%7D_x+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28123%29&bg=ffffff&fg=111111&s=0&c=20201002)
![[\hat{S}_z, \hat{S}_x] = i\hbar \hat{S}_y \qquad \qquad \qquad \qquad \qquad (124)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BS%7D_z%2C+%5Chat%7BS%7D_x%5D+%3D+i%5Chbar+%5Chat%7BS%7D_y+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28124%29&bg=ffffff&fg=111111&s=0&c=20201002)
and
![[\hat{S}_x, \hat{S}^2] = [\hat{S}_y, \hat{S}^2] = [\hat{S}_z, \hat{S}^2] = 0 \qquad \qquad \qquad \qquad \qquad (125)](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BS%7D_x%2C+%5Chat%7BS%7D%5E2%5D+%3D+%5B%5Chat%7BS%7D_y%2C+%5Chat%7BS%7D%5E2%5D+%3D+%5B%5Chat%7BS%7D_z%2C+%5Chat%7BS%7D%5E2%5D+%3D+0+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28125%29&bg=ffffff&fg=111111&s=0&c=20201002)
Focusing on the electron, and using (106)-(108) in the previous section, we have the results


where

We can also define spin raising and lowering operators  and
and  in terms of
in terms of  and
and  using (90) and (91):
using (90) and (91):


Applying these in the case of the electron using (109) and (110) in the previous section we get



and similarly



Since the  value cannot be raised and the
value cannot be raised and the  value cannot be lowered, we also have
value cannot be lowered, we also have

and

The Pauli spin matrices and matrix mechanics are normally introduced at this stage by constructing transformation matrices between distinct spin states based on the results of a rotated Stern-Gerlach apparatus. For example, after a beam of electrons is split in two in the  -direction by a Stern-Gerlach apparatus, one of the polarized beams can then be passed through a second Stern-Gerlach apparatus which is rotated by
-direction by a Stern-Gerlach apparatus, one of the polarized beams can then be passed through a second Stern-Gerlach apparatus which is rotated by  so that it is split in two in the
so that it is split in two in the 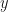 -direction. The electrons in the incoming polarized beam will be in one of the eigenstates of the
-direction. The electrons in the incoming polarized beam will be in one of the eigenstates of the  operator, which will be denoted by
operator, which will be denoted by  or
or  in what follows, whereas the electrons in an outgoing beam of the rotated apparatus will be in one of the eigenstates of the
in what follows, whereas the electrons in an outgoing beam of the rotated apparatus will be in one of the eigenstates of the  operator, which will be denoted by
operator, which will be denoted by 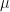 in what follows. Thus, we have the eigenvalue equations
in what follows. Thus, we have the eigenvalue equations


The operators  and
and  will both have the same measurement spectrum, namely
will both have the same measurement spectrum, namely  for
for  and
and  for
for  , but they will be referring to different and incompatible components of spin. We can now obtain transformation matrix elements
, but they will be referring to different and incompatible components of spin. We can now obtain transformation matrix elements  , i.e., probability amplitudes, for this experiment by casting the eigenvalue problem in (136) in the language of the incoming pre-prepared
, i.e., probability amplitudes, for this experiment by casting the eigenvalue problem in (136) in the language of the incoming pre-prepared  -state, and then solving it. Since all the bras and kets in this problem will have
-state, and then solving it. Since all the bras and kets in this problem will have  , we will drop this from the notation to reduce clutter. The eigenvalue problem to be solved can then be expressed as
, we will drop this from the notation to reduce clutter. The eigenvalue problem to be solved can then be expressed as

We can convert this problem into a matrix algebra problem by inserting an  -space ket-bra sum at the second vertical on the left-hand side (this ket-bra sum will then be in the space of
-space ket-bra sum at the second vertical on the left-hand side (this ket-bra sum will then be in the space of  eigenvalues):
eigenvalues):

The sum on the left can immediately be recognised as a prescription for matrix multiplication. We can deduce the matrix form of  by using (129) and (130) to write
by using (129) and (130) to write

Now, using (131) and (133) and noting that  since it is a self-space bracket, we can write
since it is a self-space bracket, we can write


Similarly, using (132) and (134) we can write

Now using (139), (140) and (141) we can finally write

The matrix on the right-hand side here is one of the three famous Pauli spin matrices. The eigenvalue problem in (138) can then be written in matrix form as

where the matrices immediately to the left and right of the equals sign contain the same elements. We immediately recognise this as a simple matrix diagonalization problem. It is straightforward to show that the eigenvalues of the Pauli spin matrix in (142) are 1 and -1, so the right-most matrix in (143) has the eigenvalues of (142) in its diagonal. This means that the transformation matrix either side of the equals sign in (143) must be the matrix whose columns are the eigenvectors corresponding to the eigenvalues. Using elementary linear algebra, this matrix of eigenvectors, normalized so that the eigenvectors are orthonormal, is easily shown to be

The absolute value squared of each element of this matrix gives the probability of an outcome of a corresponding rotated Stern-Gerlach experiment. The first column contains the probability amplitudes for the case when the pre-prepared  -state is spin-up, the second column contains the probability amplitudes for the case when the pre-prepared
-state is spin-up, the second column contains the probability amplitudes for the case when the pre-prepared  -state is spin-down. Note that the eigenvectors need to be normalized to ensure that the relevant column probabilities sum to 1.
-state is spin-down. Note that the eigenvectors need to be normalized to ensure that the relevant column probabilities sum to 1.
We can repeat this entire exercise for the case in which the Stern-Gerlach apparatus is rotated in the  -direction instead of the
-direction instead of the 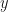 -direction, so that the relevant operators are
-direction, so that the relevant operators are  and
and  . Using completely analogous arguments, we find that
. Using completely analogous arguments, we find that

where the matrix on the right-hand side is another one of the three Pauli spin matrices. By diagonalizing this matrix, we find that the transformation matrix containing the relevant probability amplitudes for this form of the rotated Stern-Gerlach experiment is

We can repeat the exercise again assuming that the Stern-Gerlach apparatus is not rotated, so that an electron beam in a pre-prepared  -state is again passed through the apparatus oriented in the
-state is again passed through the apparatus oriented in the  -direction. In this case, using (127), we find
-direction. In this case, using (127), we find

where the matrix on the right-hand side is the final one of the three Pauli spin matrices. This matrix is already diagonalized, i.e., the eigenvalues are the elements in the main diagonal. We find that the transformation matrix containing the relevant probability amplitudes for this form of the rotated Stern-Gerlach experiment is

i.e., the identity matrix, which is not surprising given that  is a self-space bracket equal to the Kronecker delta.
is a self-space bracket equal to the Kronecker delta.
Finally, we can use (126) to deduce the matrix form of  . This is
. This is

Note that each of the transformation matrices in (144), (146) and (148) is a unitary matrix, i.e., the hermitian conjugate of the matrix equals the inverse of the matrix. This is a manifestation of the fundamental axiom of quantum mechanics that  and
and  must be connected by complex conjugation, i.e.,
must be connected by complex conjugation, i.e.,  .
.
The time-dependent Schrödinger equation and the time evolution operator
We said earlier that an event in quantum mechanics is a measurement that takes place instantaneously after a system has been prepared in a particular state. For example, a measurement of position can be made instantaneously after the system has been prepared to have a particular linear momentum state, and the probability amplitude for the position measurement would then be given by a wave function  . Immediate measurement is needed because, in general, a quantum state is time-dependent, sometimes emphasised by including the argument
. Immediate measurement is needed because, in general, a quantum state is time-dependent, sometimes emphasised by including the argument 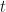 in the ket, e.g.,
in the ket, e.g.,  . If a measurement is not made instantaneously after a system is prepared in a particular state
. If a measurement is not made instantaneously after a system is prepared in a particular state  , it is a basic postulate of quantum mechanics that the system will evolve over time in accordance with the time-dependent Schrödinger equation
, it is a basic postulate of quantum mechanics that the system will evolve over time in accordance with the time-dependent Schrödinger equation

where  is the Hamiltonian operator associated with the total energy of the system. This linear first-order differential equation plays a role in quantum mechanics somewhat analogous to Newton’s second law in classical mechanics in the sense that, given an initial condition for the system, it deterministically evolves the state of the system over time from then on. It is important to note, however, that in the case of quantum mechanics this deterministic evolution only takes place in the absence of any measurement of the system. Unlike a classical system, the time evolution process ‘stops’ when a quantum mechanical system is measured. The quantum state is immediately reset to the measured value and the time evolution process then begins anew from this new state. The probabilistic aspect of quantum mechanics only arises when a measurement is made in the sense that the result of the measurement (i.e., what particular eigenvalue of the relevant Hermitian operator will end up being observed) is a random variable. The time evolution part of the process in the intervening period between measurements is what is governed by the time-dependent Schrödinger equation and is completely deterministic.
is the Hamiltonian operator associated with the total energy of the system. This linear first-order differential equation plays a role in quantum mechanics somewhat analogous to Newton’s second law in classical mechanics in the sense that, given an initial condition for the system, it deterministically evolves the state of the system over time from then on. It is important to note, however, that in the case of quantum mechanics this deterministic evolution only takes place in the absence of any measurement of the system. Unlike a classical system, the time evolution process ‘stops’ when a quantum mechanical system is measured. The quantum state is immediately reset to the measured value and the time evolution process then begins anew from this new state. The probabilistic aspect of quantum mechanics only arises when a measurement is made in the sense that the result of the measurement (i.e., what particular eigenvalue of the relevant Hermitian operator will end up being observed) is a random variable. The time evolution part of the process in the intervening period between measurements is what is governed by the time-dependent Schrödinger equation and is completely deterministic.
In order to perform calculations using the time-dependent Schrödinger equation, it is necessary to specify the relevant Hamiltonian for the system and to express the state  as a superposition of the eigenstates of the Hamiltonian. This can be achieved using a ket-bra sum. The emphasis is usually on conservative systems, i.e., systems for which the total energy is conserved over time so the Hamiltonian is time-independent,
as a superposition of the eigenstates of the Hamiltonian. This can be achieved using a ket-bra sum. The emphasis is usually on conservative systems, i.e., systems for which the total energy is conserved over time so the Hamiltonian is time-independent,  . Non-conservative systems are less tractable and require more elaborate techniques. We will only consider the conservative case here and begin by writing the typical eigenvalue equation for the Hamiltonian, i.e., the time-independent Schrödinger equation, as
. Non-conservative systems are less tractable and require more elaborate techniques. We will only consider the conservative case here and begin by writing the typical eigenvalue equation for the Hamiltonian, i.e., the time-independent Schrödinger equation, as

Given the specification of the Hamiltonian for the system, it would be necessary to solve this time-independent Schrödinger equation to find the eigenvalues and eigenstates. Using a ket-bra sum, we can express the state  as a superposition of the energy eigenstates:
as a superposition of the energy eigenstates:

Note that the eigenstates  are time-independent so the time-dependence only enters via the overlap coefficients
are time-independent so the time-dependence only enters via the overlap coefficients  in the superposition. The problem, then, is to find an explicit formula showing how these overlap coefficients change over time. To this end, we can write the full time-dependent Schrödinger equation in the energy basis given by the eigenstates of the Hamiltonian by acting on both sides of (150) with the bra
in the superposition. The problem, then, is to find an explicit formula showing how these overlap coefficients change over time. To this end, we can write the full time-dependent Schrödinger equation in the energy basis given by the eigenstates of the Hamiltonian by acting on both sides of (150) with the bra  :
:

Using the time-independence of energy eigenstates on the left-hand side and the bra form of the eigenvalue equation for the Hamiltonian on the right-hand side, this reduces to

This is a simple first-order differential equation in the overlap coefficient  which can be rearranged to read
which can be rearranged to read

Integrating both sides from an initial time 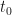 to a later time
to a later time  , and defining
, and defining  , we get
, we get

This tells us that, for a conservative system, there is a simple way to time-evolve the overlap coefficients in (152), and hence the state  as a whole, from an initial time
as a whole, from an initial time 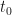 to a subsequent time
to a subsequent time  . Writing the superposition in (152) at time
. Writing the superposition in (152) at time  and using the result in (155) we get
and using the result in (155) we get

We can define a forward-displacement-in-time-by-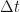 operator (time evolution operator, for short) as a function of the Hamiltonian operator by writing (156) as
operator (time evolution operator, for short) as a function of the Hamiltonian operator by writing (156) as

and interpreting the right-hand side of (157) as

Thus, in the case of a conservative system, the rule by which an initial state  evolves over time into a subsequent state
evolves over time into a subsequent state  is governed by the law of quantum mechanics expressed in (157). The initial state is simply acted upon by a time evolution operator
is governed by the law of quantum mechanics expressed in (157). The initial state is simply acted upon by a time evolution operator  , which is an exponential function of another operator, the Hamiltonian operator. Such functions of operators are to be understood as needing to be implemented via their power series expansion (another similar one is the translation in space operator, which is an exponential function of the momentum operator). Thus, we are ultimately dealing with powers of operators in these cases and we can use well-known results for manipulating powers of operators when implementing functions of operators and proving further results relating to them. For the time evolution operator, we have
, which is an exponential function of another operator, the Hamiltonian operator. Such functions of operators are to be understood as needing to be implemented via their power series expansion (another similar one is the translation in space operator, which is an exponential function of the momentum operator). Thus, we are ultimately dealing with powers of operators in these cases and we can use well-known results for manipulating powers of operators when implementing functions of operators and proving further results relating to them. For the time evolution operator, we have


where  denotes the identity. It is straightforward to show that the right-hand side of (158) results when we apply the power series form of the time evolution operator in (159) to the eigenstates of the Hamiltonian in the superposition for
denotes the identity. It is straightforward to show that the right-hand side of (158) results when we apply the power series form of the time evolution operator in (159) to the eigenstates of the Hamiltonian in the superposition for  . However, caution is needed when manipulating functions of operators such as these, as some basic algebraic relationships involving scalars do not generally hold for operators. For example, by multiplying the power series for
. However, caution is needed when manipulating functions of operators such as these, as some basic algebraic relationships involving scalars do not generally hold for operators. For example, by multiplying the power series for  and
and  and comparing the result with the power series for
and comparing the result with the power series for  , we find that it is not true that
, we find that it is not true that  unless
unless  and
and  commute. The correct general formula for combining products of two exponential functions of operators in this way is called the Baker-Campbell-Hausdorff formula. It says that
commute. The correct general formula for combining products of two exponential functions of operators in this way is called the Baker-Campbell-Hausdorff formula. It says that  , where
, where
![\hat{C} = \hat{A} + \hat{B} + \frac{1}{2} [\hat{A}, \hat{B}] + \frac{1}{12} ([\hat{A}, [\hat{A}, \hat{B}]] - [\hat{B}, [\hat{A}, \hat{B}]]) + \cdots \qquad \qquad \qquad \qquad \qquad (160)](https://s0.wp.com/latex.php?latex=%5Chat%7BC%7D+%3D++%5Chat%7BA%7D+%2B+%5Chat%7BB%7D+%2B+%5Cfrac%7B1%7D%7B2%7D+%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D+%2B+%5Cfrac%7B1%7D%7B12%7D+%28%5B%5Chat%7BA%7D%2C+%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D%5D+-+%5B%5Chat%7BB%7D%2C+%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D%5D%29+%2B+%5Ccdots+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28160%29&bg=ffffff&fg=111111&s=0&c=20201002)
This reduces to  only when
only when ![[\hat{A}, \hat{B}] = 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BA%7D%2C+%5Chat%7BB%7D%5D+%3D+0&bg=ffffff&fg=111111&s=0&c=20201002) . Since the Hamiltonian commutes with itself, we can see that the time evolution operator is a unitary operator using the basic index rule for multiplying exponential functions:
. Since the Hamiltonian commutes with itself, we can see that the time evolution operator is a unitary operator using the basic index rule for multiplying exponential functions:

From the form of the hermitian conjugate  (this is straightforward to prove by applying the algebraic rules for hermitian conjugates to the power series form of the exponential), we also note that the inverse of the time evolution operator
(this is straightforward to prove by applying the algebraic rules for hermitian conjugates to the power series form of the exponential), we also note that the inverse of the time evolution operator  in (157) is obtained simply by reversing the direction of the arrow of time.
in (157) is obtained simply by reversing the direction of the arrow of time.
We obtained the time evolution operator for a conservative system here by integrating the time-dependent Schrödinger equation (150) to arrive at (157). We could just as well have started by stating (157) as a basic postulate and deriving (150) from it as its differential form. For example, taking 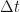 to be infinitesimally small, and writing (157) as
to be infinitesimally small, and writing (157) as

we can cast this equation into  -language by acting on both sides with the bra
-language by acting on both sides with the bra  and use the linear approximation to the exponential to get
and use the linear approximation to the exponential to get


Therefore,

or, in function notation as  ,
,

which is the wave function form of Schrödinger’s time-dependent equation.
The time evolution rule in (157) encapsulates two fundamental principles of physics, conservation of energy (a classical principle) and de Broglie’s equation  linking the energy of a quantum particle to the frequency of a wave function (a purely quantum mechanical principle). We obtained (157) for a conservative system with a time-independent Hamiltonian, meaning that the system is closed and the total energy is an invariant of the motion. In quantum mechanics, this is expressed by saying that energy eigenstates are stationary when the rule (157) is applied to them. If the ket
linking the energy of a quantum particle to the frequency of a wave function (a purely quantum mechanical principle). We obtained (157) for a conservative system with a time-independent Hamiltonian, meaning that the system is closed and the total energy is an invariant of the motion. In quantum mechanics, this is expressed by saying that energy eigenstates are stationary when the rule (157) is applied to them. If the ket  on the right hand side of (157) happens to be an eigenstate of the Hamiltonian already, say
on the right hand side of (157) happens to be an eigenstate of the Hamiltonian already, say  , then we get
, then we get

and the ket on the right hand side of (161) is the same eigenket of  as
as  up to a constant of proportionality. It yields the same eigenvalue when acted upon by
up to a constant of proportionality. It yields the same eigenvalue when acted upon by  as
as  does, and the probability of observing this eigenvalue in a measurement would remain unchanged. Thus, for a conservative system, energy eigenstates are stationary in the sense that earlier and later eigenstates of
does, and the probability of observing this eigenvalue in a measurement would remain unchanged. Thus, for a conservative system, energy eigenstates are stationary in the sense that earlier and later eigenstates of  can only differ through a phase factor so measurement probabilities remain unchanged. This will not be true in general for a ket
can only differ through a phase factor so measurement probabilities remain unchanged. This will not be true in general for a ket  on the right hand side of (157) which is not an energy eigenstate of the Hamiltonian. When this state is expressed as a superposition of energy eigenstates to obtain (158), each energy eigenstate in the superposition will have a different phase factor, i.e., the relative phases associated with each energy eigenstate change with time, so the later state
on the right hand side of (157) which is not an energy eigenstate of the Hamiltonian. When this state is expressed as a superposition of energy eigenstates to obtain (158), each energy eigenstate in the superposition will have a different phase factor, i.e., the relative phases associated with each energy eigenstate change with time, so the later state  will not generally be the same as the earlier state
will not generally be the same as the earlier state  to within a phase factor. De Broglie’s equation comes into the story because we can rewrite
to within a phase factor. De Broglie’s equation comes into the story because we can rewrite  as
as  , where
, where  is the angular frequency of a wave associated with the energy
is the angular frequency of a wave associated with the energy 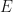 . Thus, the phase factors arising from applying the time evolution operator for a conservative system have the form
. Thus, the phase factors arising from applying the time evolution operator for a conservative system have the form  . With every energy
. With every energy 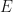 there is to be associated a unique single frequency
there is to be associated a unique single frequency  , and (158) shows that the eigenstates of energy evolve over time at this fixed frequency.
, and (158) shows that the eigenstates of energy evolve over time at this fixed frequency.
To give some applied examples of calculations involving the time evolution operator, consider a beam of neutrons entering a region of uniform magnetic field at time  . Although a neutron does not have charge, it does have a magnetic dipole moment and a spin angular momentum index
. Although a neutron does not have charge, it does have a magnetic dipole moment and a spin angular momentum index  (same as the electron). Suppose the beam of incoming neutrons is prepared with a known
(same as the electron). Suppose the beam of incoming neutrons is prepared with a known 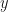 -direction spin component and travels in the
-direction spin component and travels in the  -direction. At
-direction. At  , it enters the region of uniform magnetic field
, it enters the region of uniform magnetic field  pointing in the
pointing in the  -direction. In classical physics, the potential energy that would be associated in this situation with a magnetic dipole moment
-direction. In classical physics, the potential energy that would be associated in this situation with a magnetic dipole moment  in a magnetic field
in a magnetic field  is
is  . (To get an idea of why this is the case, recall from (118) that the torque experienced by the magnetic dipole moment in the magnetic field is
. (To get an idea of why this is the case, recall from (118) that the torque experienced by the magnetic dipole moment in the magnetic field is  . The work done in aligning this with the magnetic field is
. The work done in aligning this with the magnetic field is  . Therefore, the potential energy is
. Therefore, the potential energy is  ). There is no kinetic energy because the magnetic force is always perpendicular to the velocity. Thus, in the classical case, the Hamiltonian would be
). There is no kinetic energy because the magnetic force is always perpendicular to the velocity. Thus, in the classical case, the Hamiltonian would be  . By analogy, the Hamiltonian operator expressing the energy of the neutron magnetic dipole moment in the magnetic field pointing in the
. By analogy, the Hamiltonian operator expressing the energy of the neutron magnetic dipole moment in the magnetic field pointing in the  -direction would be
-direction would be

where 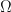 represents a collection of parameters which together carry the dimensions of angular frequency. Suppose a neutron enters the magnetic field at time
represents a collection of parameters which together carry the dimensions of angular frequency. Suppose a neutron enters the magnetic field at time  in a spin state
in a spin state  . This is the initial state of the system, i.e., the state
. This is the initial state of the system, i.e., the state  in (157). It is an eigenstate of the spin angular momentum operator
in (157). It is an eigenstate of the spin angular momentum operator  with eigenvalue
with eigenvalue  , as defined by (136). This initial neutron state will evolve over time in accordance with (157) into a later state
, as defined by (136). This initial neutron state will evolve over time in accordance with (157) into a later state  given by
given by

But the state  is not an eigenstate of the Hamiltonian in (162). The eigenstates of the Hamiltonian are those of
is not an eigenstate of the Hamiltonian in (162). The eigenstates of the Hamiltonian are those of  , defined by (135). We now need to expand
, defined by (135). We now need to expand  in a superposition of the Hamiltonian’s eigenstates using a ket-bra sum. We write
in a superposition of the Hamiltonian’s eigenstates using a ket-bra sum. We write


where  labels the eigenstates of
labels the eigenstates of  and thus of
and thus of  . We need the overlap coefficients
. We need the overlap coefficients  appearing in the superposition (164), but these are exactly the ones calculated in (144), in the first column. Thus, we can write the superposition as
appearing in the superposition (164), but these are exactly the ones calculated in (144), in the first column. Thus, we can write the superposition as

Applying the time evolution operator to this as in the right-hand side of (163) we obtain

We see from (166) that  is not the same state as
is not the same state as  up to a phase factor, so this is an example of a nonstationary state. The relative phases associated with each energy eigenstate have changed with time.
up to a phase factor, so this is an example of a nonstationary state. The relative phases associated with each energy eigenstate have changed with time.
Given that the system is initially in the  eigenstate
eigenstate  at time
at time 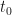 , suppose we want to know the probability amplitude to find it in the
, suppose we want to know the probability amplitude to find it in the  eigenstate
eigenstate  at a later time
at a later time  . We can apply the bra
. We can apply the bra  to the time-evolved ket in (166) to get
to the time-evolved ket in (166) to get

We observe that the absolute value squared of (167) is the same as we would get if we had applied the bra  to the initial state in (165). Thus, the probability of finding the spin up state in the
to the initial state in (165). Thus, the probability of finding the spin up state in the  -direction does not vary with time, i.e., it is a stationary state, confirming that this spin up state is an eigenstate of energy.
-direction does not vary with time, i.e., it is a stationary state, confirming that this spin up state is an eigenstate of energy.
By way of contrast, suppose again that the system is initially in the  eigenstate
eigenstate  at time
at time  , but now we want to know the probability amplitude to find it still in the
, but now we want to know the probability amplitude to find it still in the  eigenstate
eigenstate  at a later time
at a later time  . We can apply the bra
. We can apply the bra  to the time-evolved ket in (166) to get
to the time-evolved ket in (166) to get


But the overlap coefficients in (168) are just the complex conjugates of the entries in the first column of (144), so we have



Therefore, the probability of finding the initial spin state again at time  is
is

We find that the probability amplitude in (169) oscillates in time at frequency  , and the probability in (170) varies sinusoidally over time at frequency
, and the probability in (170) varies sinusoidally over time at frequency  . Thus, even if we end up at
. Thus, even if we end up at  observing the same state
observing the same state  that we started with at
that we started with at  , the state
, the state  is not stationary, since the passage of time causes variation in the relative phase differences among the energy eigenstates in the superposition and this causes the probability of this outcome to vary with time.
is not stationary, since the passage of time causes variation in the relative phase differences among the energy eigenstates in the superposition and this causes the probability of this outcome to vary with time.
Another important mathematical idea in this area of quantum mechanics is that of calculating how the average value of an operator changes with time. This leads to the concepts of the classical limit of quantum mechanics and invariant operators of a quantum system which always give stationary measurement results. Consider an operator  which represents some measurement observable and has the eigenvalue equation
which represents some measurement observable and has the eigenvalue equation  . Suppose a quantum system is prepared at time
. Suppose a quantum system is prepared at time  to be in some quantum state
to be in some quantum state  which is not an eigenstate of
which is not an eigenstate of  . With a view to applying
. With a view to applying  to
to  , we can expand the latter as a superposition of the eigenstates of
, we can expand the latter as a superposition of the eigenstates of  :
:

Then applying  to this gives us a new state expressed as a superposition:
to this gives us a new state expressed as a superposition:

To perform probability calculations using (172) we would need to cast it in a relevant language by applying a suitable bra to both sides. In particular, casting (172) in the language of  gives us the expected value of the operator
gives us the expected value of the operator  , denoted by
, denoted by  :
:

This corresponds to applying  to the state
to the state  instantaneously after the latter is prepared, repeating this experiment a large number of times to obtain many results from the spectrum of possible
instantaneously after the latter is prepared, repeating this experiment a large number of times to obtain many results from the spectrum of possible  -values, and then working out the average of
-values, and then working out the average of  from the experimental data. But suppose there is a time delay between preparing the state
from the experimental data. But suppose there is a time delay between preparing the state  and making the repeated measurements of
and making the repeated measurements of  , so that instead of making each measurement at
, so that instead of making each measurement at  we make it at a later time
we make it at a later time  . Then by (157) the state
. Then by (157) the state  will have evolved to a state
will have evolved to a state  by the time each measurement is made, where
by the time each measurement is made, where  is given by
is given by

Using the time-reversed operator  , we can write the expected value of
, we can write the expected value of  at time
at time  as
as

Differentiating (175) with respect to time then allows us to study how the average value of an operator changes with time. Using the product rule, we get
![\frac{\partial}{\partial \Delta t} [\exp (i \Delta t \hat{H} /\hbar) \hat{A} \exp (- i \Delta t \hat{H} /\hbar)]](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+%5CDelta+t%7D+%5B%5Cexp+%28i+%5CDelta+t+%5Chat%7BH%7D+%2F%5Chbar%29+%5Chat%7BA%7D+%5Cexp+%28-+i+%5CDelta+t+%5Chat%7BH%7D+%2F%5Chbar%29%5D&bg=ffffff&fg=111111&s=0&c=20201002)



![= \exp (i \Delta t \hat{H} /\hbar) \big(\frac{\partial \hat{A}}{\partial t} + \frac{1}{i \hbar} [\hat{A}, \hat{H}]\big) \exp (-i \Delta t \hat{H} /\hbar) \qquad \qquad \qquad \qquad \qquad (176)](https://s0.wp.com/latex.php?latex=%3D+%5Cexp+%28i+%5CDelta+t+%5Chat%7BH%7D+%2F%5Chbar%29+%5Cbig%28%5Cfrac%7B%5Cpartial+%5Chat%7BA%7D%7D%7B%5Cpartial+t%7D+%2B+%5Cfrac%7B1%7D%7Bi+%5Chbar%7D+%5B%5Chat%7BA%7D%2C+%5Chat%7BH%7D%5D%5Cbig%29+%5Cexp+%28-i+%5CDelta+t+%5Chat%7BH%7D+%2F%5Chbar%29+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28176%29&bg=ffffff&fg=111111&s=0&c=20201002)
Using (176) with (175) we deduce that
![\frac{d}{dt} \langle \beta | \hat{A} | \beta \rangle = \langle \beta | \big(\frac{\partial \hat{A}}{\partial t} + \frac{1}{i \hbar} [\hat{A}, \hat{H}]\big) | \beta \rangle \qquad \qquad \qquad \qquad \qquad (177)](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdt%7D+%5Clangle+%5Cbeta+%7C+%5Chat%7BA%7D+%7C+%5Cbeta+%5Crangle+%3D+%5Clangle+%5Cbeta+%7C+%5Cbig%28%5Cfrac%7B%5Cpartial+%5Chat%7BA%7D%7D%7B%5Cpartial+t%7D+%2B+%5Cfrac%7B1%7D%7Bi+%5Chbar%7D+%5B%5Chat%7BA%7D%2C+%5Chat%7BH%7D%5D%5Cbig%29+%7C+%5Cbeta+%5Crangle+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28177%29&bg=ffffff&fg=111111&s=0&c=20201002)
What (177) is telling us is that the time derivative of  is actually the average of a new operator bracketed between the same states. The new operator consists of two terms. The first term is the time derivative of the operator itself. This is often taken to be zero because it is unusual to have time-varying measurement apparatus in an experiment. In the case of the Stern-Gerlach experiments, for example, an operator with a non-zero time derivative would correspond to something like the apparatus continually revolving while the measurements were being made. In the following, we will always assume
is actually the average of a new operator bracketed between the same states. The new operator consists of two terms. The first term is the time derivative of the operator itself. This is often taken to be zero because it is unusual to have time-varying measurement apparatus in an experiment. In the case of the Stern-Gerlach experiments, for example, an operator with a non-zero time derivative would correspond to something like the apparatus continually revolving while the measurements were being made. In the following, we will always assume  . The second term of the new operator in (177) is the commutator of
. The second term of the new operator in (177) is the commutator of  with
with  . The key point here is that the average value of a fixed measurement observable
. The key point here is that the average value of a fixed measurement observable  will change over time if
will change over time if ![[\hat{A}, \hat{H}] \neq 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BA%7D%2C+%5Chat%7BH%7D%5D+%5Cneq+0&bg=ffffff&fg=111111&s=0&c=20201002) .
.
Something called the Correspondence Principle in quantum mechanics suggests that, in the case ![[\hat{A}, \hat{H}] \neq 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BA%7D%2C+%5Chat%7BH%7D%5D+%5Cneq+0&bg=ffffff&fg=111111&s=0&c=20201002) , the average of
, the average of  should evolve over time in accordance with a Newtonian-like equation of motion. The famous Ehrenfest Theorem, for example, is a specific case of this involving position and momentum operators. Consider a particle in a potential
should evolve over time in accordance with a Newtonian-like equation of motion. The famous Ehrenfest Theorem, for example, is a specific case of this involving position and momentum operators. Consider a particle in a potential  for which the Hamiltonian is
for which the Hamiltonian is

Taking first  and then
and then  in (177) with
in (177) with  , and using the results
, and using the results ![\langle x | [\hat{p}, \hat{V}] = -i \hbar (dV/dx) \langle x |](https://s0.wp.com/latex.php?latex=%5Clangle+x+%7C+%5B%5Chat%7Bp%7D%2C+%5Chat%7BV%7D%5D+%3D+-i+%5Chbar+%28dV%2Fdx%29+%5Clangle+x+%7C&bg=ffffff&fg=111111&s=0&c=20201002) and
and ![[\hat{x}, \hat{p}^2] = 2 i \hbar \hat{p}](https://s0.wp.com/latex.php?latex=%5B%5Chat%7Bx%7D%2C+%5Chat%7Bp%7D%5E2%5D+%3D+2+i+%5Chbar+%5Chat%7Bp%7D&bg=ffffff&fg=111111&s=0&c=20201002) , we obtain the Newtonian-like equations of motion
, we obtain the Newtonian-like equations of motion
![\frac{d}{dt} \langle \hat{x} \rangle = \frac{d}{dt} \langle x | \hat{x} | x \rangle = \langle x | \frac{1}{i\hbar} [\hat{x}, \hat{H}] | x \rangle](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdt%7D+%5Clangle+%5Chat%7Bx%7D+%5Crangle+%3D+%5Cfrac%7Bd%7D%7Bdt%7D+%5Clangle+x+%7C+%5Chat%7Bx%7D+%7C+x+%5Crangle+%3D+%5Clangle+x+%7C+%5Cfrac%7B1%7D%7Bi%5Chbar%7D+%5B%5Chat%7Bx%7D%2C+%5Chat%7BH%7D%5D+%7C+x+%5Crangle&bg=ffffff&fg=111111&s=0&c=20201002)
![= \frac{1}{i\hbar} \langle x | \big[\hat{x}, \frac{\hat{p}^2}{2m} \big] | x \rangle = \frac{1}{m} \langle x | \hat{p} | x \rangle = \frac{1}{m} \langle \hat{p} \rangle \qquad \qquad \qquad \qquad \qquad (178)](https://s0.wp.com/latex.php?latex=%3D+%5Cfrac%7B1%7D%7Bi%5Chbar%7D+%5Clangle+x+%7C+%5Cbig%5B%5Chat%7Bx%7D%2C+%5Cfrac%7B%5Chat%7Bp%7D%5E2%7D%7B2m%7D+%5Cbig%5D+%7C+x+%5Crangle+%3D+%5Cfrac%7B1%7D%7Bm%7D+%5Clangle+x+%7C+%5Chat%7Bp%7D+%7C+x+%5Crangle+%3D+%5Cfrac%7B1%7D%7Bm%7D+%5Clangle+%5Chat%7Bp%7D+%5Crangle+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28178%29&bg=ffffff&fg=111111&s=0&c=20201002)
and
![\frac{d}{dt} \langle \hat{p} \rangle = \frac{d}{dt} \langle x | \hat{p} | x \rangle = \langle x | \frac{1}{i\hbar} [\hat{p}, \hat{H}] | x \rangle](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdt%7D+%5Clangle+%5Chat%7Bp%7D+%5Crangle+%3D+%5Cfrac%7Bd%7D%7Bdt%7D+%5Clangle+x+%7C+%5Chat%7Bp%7D+%7C+x+%5Crangle+%3D+%5Clangle+x+%7C+%5Cfrac%7B1%7D%7Bi%5Chbar%7D+%5B%5Chat%7Bp%7D%2C+%5Chat%7BH%7D%5D+%7C+x+%5Crangle&bg=ffffff&fg=111111&s=0&c=20201002)
![= \frac{1}{i\hbar} \langle x | [\hat{p}, V(\hat{x}) ] | x \rangle = \langle x | -(dV/dx) | x \rangle = -\langle dV/dx \rangle \qquad \qquad \qquad \qquad \qquad (179)](https://s0.wp.com/latex.php?latex=%3D+%5Cfrac%7B1%7D%7Bi%5Chbar%7D+%5Clangle+x+%7C+%5B%5Chat%7Bp%7D%2C+V%28%5Chat%7Bx%7D%29+%5D+%7C+x+%5Crangle+%3D+%5Clangle+x+%7C+-%28dV%2Fdx%29+%7C+x+%5Crangle+%3D+-%5Clangle+dV%2Fdx+%5Crangle+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%5Cqquad+%28179%29&bg=ffffff&fg=111111&s=0&c=20201002)
In the case  and
and ![[\hat{A}, \hat{H}] = 0](https://s0.wp.com/latex.php?latex=%5B%5Chat%7BA%7D%2C+%5Chat%7BH%7D%5D+%3D+0&bg=ffffff&fg=111111&s=0&c=20201002) , we would have a stationary time average, i.e.,
, we would have a stationary time average, i.e.,  . Such operators represent conserved quantities, formally called invariants of the system. For example, the energy of a closed system is such an invariant, as we saw above. Another example of an invariant operator in the context of the neutron in a magnetic field is the case
. Such operators represent conserved quantities, formally called invariants of the system. For example, the energy of a closed system is such an invariant, as we saw above. Another example of an invariant operator in the context of the neutron in a magnetic field is the case  . The total spin angular momentum operator is not a function of time and it commutes with the Hamiltonian specified in (162) so it must be an invariant of the system. By (126), we have
. The total spin angular momentum operator is not a function of time and it commutes with the Hamiltonian specified in (162) so it must be an invariant of the system. By (126), we have  and this must be preserved in the magnetic field, fundamentally because the magnetic field cannot change the neutron’s spin parameter
and this must be preserved in the magnetic field, fundamentally because the magnetic field cannot change the neutron’s spin parameter  . In contrast, the operator
. In contrast, the operator  with the eigenvalue equation given in (136) does not commute with the Hamiltonian in (162) so it cannot be an invariant of the system. A neutron entering the system in a pre-prepared spin up state
with the eigenvalue equation given in (136) does not commute with the Hamiltonian in (162) so it cannot be an invariant of the system. A neutron entering the system in a pre-prepared spin up state  can be found at the exit in a spin down state
can be found at the exit in a spin down state  .
.
and
are constants and
is a standard Wiener process. I used the Euler–Maruyama method with a time step of
in Python to generate and plot a sample path of this process from
up to
, setting the initial position as
and the values
and
. The following picture shows this sample path:
parameter in the drift term of the SDE, which tends to pull the process back down when
goes above zero and back up when
goes below zero.
. From (2) we then get
from the normalisation condition
we can rewrite (4) as
, we have
and
. Using these substitutions together with the expression for
in (5) above we get

,
and
might be difficult to evaluate manually, but in the case of the Ornstein-Uhlenbeck process these three integrals have simple exact values. For
in (6), we use the well-known trick of solving the double integral
and
, with limits
to
for
and
to
for
, and the Cartesian area element
becoming the polar coordinates area element
, the double integral becomes
, we conclude
. It is easily shown that
, and we can calculate
by integrating
by parts:
sample paths of the Ornstein-Uhlenbeck process
with the same specifications as the plot above, and plotted the mean
and mean squared distance
as functions of time together with the corresponding exact values. The plots below show that for sufficiently long times the numerical calculations do indeed fluctuate around the values predicted on the basis of the stationary pdf derived above:

evaluated at
using the
simulated sample paths, and plotted it together with the stationary pdf,
, derived above from the Fokker-Planck equation. The plot below shows good agreement between the two: